(本小题12分)如图, 一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子? 请说明理由.请用你的计算数据说明理由。(冰、水的体积差异忽略不计)(π取3.14)
本小题满分12分)设函数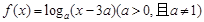 ,当点
,当点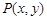 是函数
是函数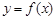 图象上的点
图象上的点 时,点
时,点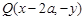 是函数
是函数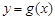 图象上的点.
图象上的点.
(1)写出函数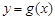 的解析式;
的解析式;
(2)若当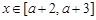 时,恒有
时,恒有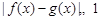 ,试确定
,试确定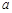 的取值范围;
的取值范围;
(3)把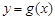 的图象向左平移
的图象向左平移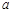 个单位得到
个单位得到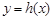 的图象,函数
的图象,函数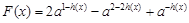
 ,(
,(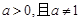 )在
)在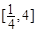 的最大值为
的最大值为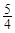 ,求
,求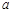 的值
的值
本小题满分10分)设函数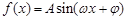 (
(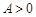 ,
,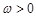 ,
,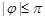 )的图象的最高点D的坐标为
)的图象的最高点D的坐标为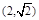 ,由最高点运动到相邻的最低点F时,曲线与
,由最高点运动到相邻的最低点F时,曲线与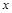 轴相交于点
轴相交于点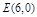 .
.
(1)求A、ω、φ的值;
(2)求函数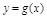 ,使其图象与
,使其图象与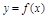 图象关于直线
图象关于直线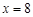 对称.
对称.
(本小题满分10分)已知定义域为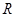 的函数
的函数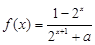 是奇函数.
是奇函数.
(1)求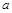 的值;
的值;
(2)若对任意的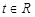 ,不等式
,不等式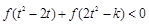 恒成立,求实数
恒成立,求实数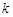 的取值范围.
的取值范围.
(本小题满分10分)如图是总体的一个样本频率分布直方图,且在[15,18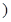 内频数为8.
内频数为8.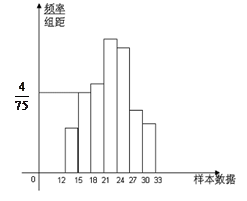
(1)求样本在[15,18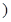 内的频率;
内的频率;
(2)求样本容量;
(3)若在[12,15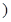 内的小矩形面积为0.06,求在[18,33
内的小矩形面积为0.06,求在[18,33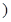 内的频数.
内的频数.
对任意 ,函数
,函数 的值恒大于零,求
的值恒大于零,求 的取值范围.
的取值范围.