本小题满分10分)设函数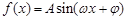 (
(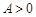 ,
,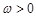 ,
,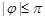 )的图象的最高点D的坐标为
)的图象的最高点D的坐标为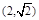 ,由最高点运动到相邻的最低点F时,曲线与
,由最高点运动到相邻的最低点F时,曲线与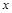 轴相交于点
轴相交于点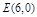 .
.
(1)求A、ω、φ的值;
(2)求函数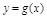 ,使其图象与
,使其图象与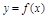 图象关于直线
图象关于直线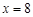 对称.
对称.
(本小题12分)为了丰富学生的课余生活,促进校园文化建设,我校高二年级通过预赛选出了6个班(含甲、乙)进行经典美文颂读比赛决赛.决赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)决赛中甲、乙两班之间的班级数记为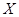 ,求
,求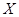 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
在极坐标系中,已知圆C的圆心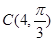 ,半径r=2,Q点在圆C上运动。
,半径r=2,Q点在圆C上运动。
(I)求圆C的极坐标方程;
(II)若P在直线OQ上运动,且OQ∶OP=3∶2,求动点P的轨迹方程。
(本小题满分12分)已知点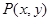 是圆
是圆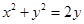 上的动点,
上的动点,
(1)求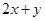 的取值范围;
的取值范围;
(2)若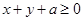 恒成立,求实数
恒成立,求实数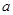 的取值范围。
的取值范围。
(本小题满分12分)
若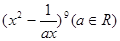 的展开式中
的展开式中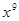 的系数是
的系数是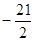 .
.
(1)求展开式中的常数项;
(2)求 的值.
的值.
已知等差数列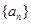 的前
的前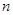 项和为
项和为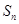 ,且
,且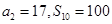 .
.
(I)求数列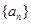 的通项公式;
的通项公式;
(II)若数列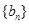 满足
满足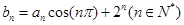 ,求数列
,求数列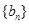 的前
的前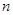 项和.
项和.