(本小题满分12分)
在极坐标系中,已知圆C的圆心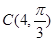 ,半径r=2,Q点在圆C上运动。
,半径r=2,Q点在圆C上运动。
(I)求圆C的极坐标方程;
(II)若P在直线OQ上运动,且OQ∶OP=3∶2,求动点P的轨迹方程。
(本小题满分14分)
已知函数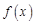 和
和 的图象关于原
的图象关于原 点对称,且
点对称,且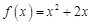 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)解不等式 ;
;
(Ⅲ)若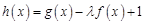 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数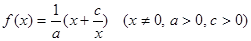 ,当
,当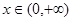 时,函数
时,函数 在x=2处取得最小值1。
在x=2处取得最小值1。
(1)求函数
 的解析式;
的解析式;
(2)设k>0,解关于x的不等式 。
。
(本小题满分12分)
已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当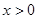 时,
时,
(1)求 的解析式;
的解析式;
(2)讨论函数 的单调性,并求
的单调性,并求 的值域。
的值域。
(本题满分12分)
在一个不透明的盒子中,放有标号分别为1,2,3的三个大小相同的小球,现从这个盒子中,有放回地先后取得两个小球,其标号分别为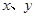 ,记
,记 .
.
(1)求随机变量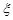 的最大值,并求事件“
的最大值,并求事件“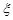 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量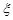 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)设集合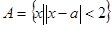 、
、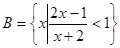 ,全集为R
,全集为R
(1)当a=1时,求: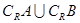 ;
;
(2)若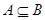 ,求实数
,求实数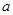 的取值范围。
的取值范围。