(本小题满分12分)已知某公司生产品牌服装的年固定成本是10万元,每生产一千件,需另投入2.7万元,设该公司年内共生产该品牌服装 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式
(千件)的函数解析式
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大?
(注:年利润=年销售收入 年总成本)
年总成本)
已知命题p:“ x∈[1,2],2x2-a≥0”,命题q:“
x∈[1,2],2x2-a≥0”,命题q:“ x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
已知全集 R,
R, ,
, .
.
(1)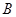

 ;
;
(2)若不等式 的解集为
的解集为 ,求
,求 、
、 的值
的值
设函数f(x)=lnx-ax+ -1.
-1.
(1) 当a=1时, 过原点的直线与函数f(x)的图象相切于点P, 求点P的坐标;
(2) 当0<a< 时, 求函数f(x)的单调区间;
时, 求函数f(x)的单调区间;
(3) 当a= 时, 设函数g(x)=x2-2bx-
时, 设函数g(x)=x2-2bx-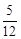 , 若对于
, 若对于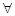 x1∈
x1∈ ,
, 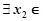 [0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<
[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<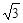 +1).
+1).
已知点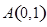 、
、 ,
, 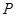 是一个动点, 且直线
是一个动点, 且直线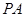 、
、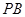 的斜率之积为
的斜率之积为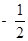 .
.
(1) 求动点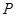 的轨迹
的轨迹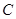 的方程;
的方程;
(2) 设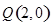 , 过点
, 过点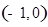 的直线
的直线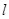 交
交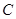 于
于 、
、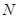 两点, 若对满足条件的任意直线
两点, 若对满足条件的任意直线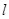 , 不等式
, 不等式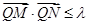 恒成立, 求
恒成立, 求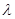 的最小值.
的最小值.
已知函数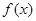
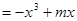 在
在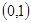 上是增函数
上是增函数
(1)求实数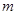 的取值集合
的取值集合
(2)当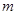 取值集合
取值集合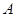 中的最小值时, 定义数列
中的最小值时, 定义数列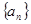 ;满足
;满足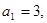 且
且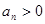 ,
,  , 设
, 设 , 证明:数列
, 证明:数列 是等比数列, 并求数列
是等比数列, 并求数列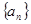 的通项公式.
的通项公式.
(3)若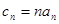 , 数列
, 数列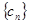 的前
的前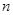 项和为
项和为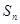 , 求
, 求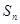 .
.