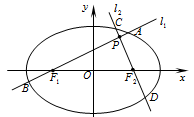
(本小题13分)如图,分别过椭圆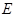 :
: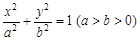 左右焦点
左右焦点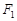 、
、 的动直线
的动直线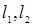 相交于
相交于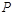 点,与椭圆
点,与椭圆 分别交于
分别交于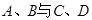 不同四点,直线
不同四点,直线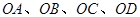 的斜率
的斜率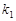 、
、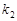 、
、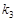 、
、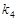 满足
满足 .已知当
.已知当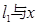 轴重合时,
轴重合时,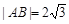 ,
,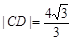 .
.
(1)求椭圆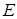 的方程;
的方程;
(2)是否存在定点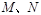 ,使得
,使得 为定值.若存在,求出
为定值.若存在,求出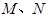 点坐标并求出此定值,若不存在,说明理由.
点坐标并求出此定值,若不存在,说明理由.
据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本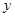 (万元)可以看成月产量
(万元)可以看成月产量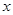 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本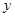 (万元)关于月产量
(万元)关于月产量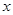 (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
已知数列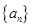 的各项均满足
的各项均满足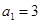 ,
,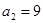 ,
,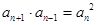
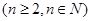
(1)求数列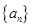 的通项公式;
的通项公式;
(2)设数列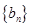 的通项公式是
的通项公式是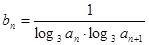 ,前
,前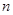 项和为
项和为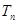 ,
,
求证:对于任意的正数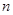 ,总有
,总有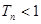 .
.
在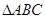 中,
中,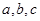 分别是角
分别是角 的对边,且
的对边,且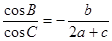 .
.
(1)求角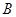 的大小;
的大小;
(2)若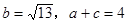 ,求
,求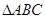 的面积.
的面积.
命题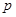 :实数
:实数 满足
满足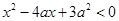 ,其中
,其中 ,命题
,命题 :实数
:实数 满足
满足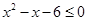 或
或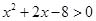 ,且
,且  是
是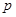 的必要不充分条件,求
的必要不充分条件,求 的取值范围.
的取值范围.
已知椭圆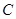 :
: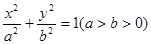 的离心率为
的离心率为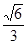 ,右焦点为(
,右焦点为( ,0).
,0).
(1)求椭圆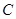 的方程;
的方程;
(2)若过原点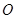 作两条互相垂直的射线,与椭圆交于
作两条互相垂直的射线,与椭圆交于 ,
,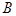 两点,求证:点
两点,求证:点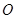 到直线
到直线 的距离为定值.
的距离为定值.