光滑水平面与一半径为R＝2.5 m的竖直光滑圆轨道平滑连接，如图所示，物体可以由圆轨道底端阀门(图中未画出)进入圆轨道，水平轨道上有一轻质弹簧，其左端固定在墙壁上，右端与质量为m＝0.5 kg的小球A接触但不相连，今向左推小球A压缩弹簧至某一位置后，由静止释放小球A，测得小球A到达圆轨道最高点时对轨道的压力大小为FN＝10 N，g＝10 m/s2.
(1)求弹簧的弹性势能Ep；
(2)若弹簧的弹性势能Ep＝25 J，小球进入圆轨道后阀门关闭，通过计算说明小球会不会脱离圆轨道．若脱离，求在轨道上何处脱离(可用三角函数表示)，若不能脱离，求小球对轨道的最大与最小压力的差ΔF.
某学习小组利用大食拉油圆桶（去掉上半部）、小石子A来测定水的折射率，如图所示。当桶内没有水时，从某点B恰能看到桶底边缘的某点C；当桶内水的深度等于桶高的一半时，仍沿BC方向看去，恰好看到桶底上的小石子A，A在圆桶的底面直径CD上。用毫米刻度尺测得直径CD=16.00cm，桶高DE=12.00cm，距离AC=3.50cm。光在真空中的传播速度为c
,求水的折射率n和光在水中的传播速度v。
某地强风速v=10m/s，空气的密度
。若通过截面积S=400m2的风能全部用于使风力发电机转动，且风能的20%转化为电能，则通过这个截面的风的发电功率是多大？
如图所示，一位质量m=60kg参加“江苏调考在一次消防逃生演练中，队员从倾斜直滑道AB的顶端A由静止滑下，经B点后水平滑出，最后落在水平地面的护垫上（不计护垫厚度的影响）。已知A、B离水平地面的高度分别为H=6.2m、h＝3.2m，A、B两点间的水平距离为L=4.0m，队员与滑道间的动摩擦因数μ＝0.3，g取10m/s2。求：
⑴队员到达B点的速度大小；
⑵队员落地点到B点的水平距离；
⑶队员自顶端A至落地所用的时间。
如图所示，一光滑的半径为R的半圆形轨道放在水平面上，B点在A点的正上方，一个质量为m的小球以某一速度冲上轨道，当小球到达B点时，小球对轨道的压力恰好为零。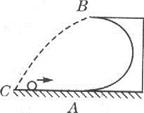
（1）求小球到达B点时的速度？
（2）求小球落地点C距A处多远?
已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v1的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行周期T。