（本题6分）某校从甲乙两名优秀选手中选一名选手参加全市中学生田径百米比赛（100米记录为12.2秒，通常情况下成绩为12.5秒可获冠军）。该校预先对这两名选手测试了8次，测试成绩如下表：
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 选手甲成绩（秒） |
12.1 |
12.4 |
12.8 |
12.5 |
13 |
12.6 |
12.4 |
12.2 |
| 选手乙成绩（秒） |
12 |
11.9 |
12.8 |
13 |
13.2 |
12.8 |
11.8 |
12.5 |
根据测试成绩，请你运用所学过的统计知识做出合理的判断，派哪一位选手参加比赛更好？为什么？
如图，点E，F分别是锐角∠A两边上的点，AE=AF，分别以点E，F为圆心，以AE的长为半径画弧，两弧相交于点D，连接DE，DF．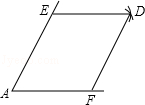
（1）请你判断所画四边形的形状，并说明理由；
（2）连接EF，若AE=8厘米，∠A=60°，求线段EF的长．
如图①，在矩形ABCD中，AB=
，BC=3，在BC边上取两点E、F（点E在点F的左边），以EF为边所作等边△PEF，顶点P恰好在AD上，直线PE、PF分别交直线AC于点G、H．
（1）求△PEF的边长；
（2）若△PEF的边EF在线段CB上移动，试猜想：PH与BE有何数量关系？并证明你猜想的结论；
（3）若△PEF的边EF在射线CB上移动（分别如图②和图③所示，CF＞1，P不与A重合），（2）中的结论还成立吗？若不成立，直接写出你发现的新结论．
直线y=x+b与双曲线y=
交于点A（﹣1，﹣5）．并分别与x轴、y轴交于点C、B．
（1）直接写出b= ，m= ；
（2）根据图象直接写出不等式x+b＜的解集为 ；
（3）若点D在x轴的正半轴上，是否存在以点D、C、B构成的三角形与△OAB相似？若存在，请求出D的坐标；若不存在，请说明理由．
如图，在正方形ABCD中，点E、F分别在BC和CD上，AE=AF．
（1）求证：BE=DF
（2）连接AC交EF于点D，延长OC至点M，使OM=OA，连结EM、FM，试证明四边形AEMF是菱形．
如图，一次函数y1=mx+n的图象与x轴、y轴分别交于A、B两点，与反比例函数y2=
（x＜0）交于点C，过点C分别作x轴、y轴的垂线，垂足分别为点E、F．若OB=2，CF=6，
．
（1）求点A的坐标；
（2）求一次函数和反比例函数的表达式．