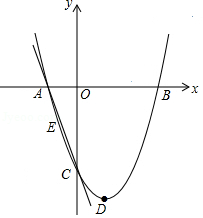
（本题12分）如图甲，在平面直角坐标系中，直线y=
x+8分别交x轴、y轴于点A、B，⊙O的半径为2
个单位长度．点P为直线y=x+8上的动点，过点P作⊙O的切线PC、PD，切点分别为C、D，且PC⊥PD．
（1）试说明四边形OCPD的形状（要有证明过程）；
（2）求点P的坐标；
（3）如图乙，若直线y=x+b将⊙O的圆周分成两段弧长之比为1：3，请直接写出b的值
（4）向右移动⊙O（圆心O始终保持在x轴上），试求出当⊙O与直线y=x+8有交点时圆心O的横坐标m的取值范围。
为了对学生进行革命传统教育，红旗中学开展了“清明节祭扫”活动．全校学生从学校同时出发，步行4000米到达烈士纪念馆．学校要求九（1）班提前到达目的地，做好活动的准备工作．行走过程中，九（1）班步行的平均速度是其他班的1.25倍，结果比其他班提前10分钟到达．分别求九（1）班、其他班步行的平均速度．
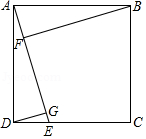
如图， 是正方形， 是 边上任意一点，连接 ，作 ， ，垂足分别为 ， ．求证： ．
解不等式组 ．
先化简，再求值．
，其中 ， ．
如图，抛物线 的图象经过点 ，顶点 的坐标为 ，与 轴交于 、 两点．
（1）求抛物线的解析式．
（2）连接 ， 为直线 上一点，当 时，求点 的坐标和 的值．
（3）点 是 轴上一动点，当 为何值时， 的值最小．并求出这个最小值．
（4）点 关于 轴的对称点为 ，当 取最小值时，在抛物线的对称轴上是否存在点 ，使 是直角三角形？若存在，请求出点 的坐标；若不存在，请说明理由．
