已知P是圆M:x2+y2+4x+4-4m2=0(m>0且m≠2)上任意一点,点N的坐标为(2,0),线段NP的垂直平分线交直线MP于点Q,当点P在圆M上运动时,点Q的轨迹为C.
(1)求出轨迹C的方程,并讨论曲线C的形状;
(2)当m= 时,在x轴上是否存在一定点E,使得对曲线C的任意一条过E的弦AB,
时,在x轴上是否存在一定点E,使得对曲线C的任意一条过E的弦AB, 为定值?若存在,求出定点和定值;若不存在,请说明理由.
为定值?若存在,求出定点和定值;若不存在,请说明理由.
在某学校组织的一次篮球定点投篮训练中,规定每人最多投3次:在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次。某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为
| ξ |
0 |
2 |
3 |
4 |
5 |
| P |
0.03 |
P1 |
P2 |
P3 |
P4 |
(1)求q2的值;
(2)求随机变量ξ的数学期望E(ξ);
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1= a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.
a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.
(1)求证:CD⊥面ABB1A1;
(2)在侧棱BB1上确定一点E,使得二面角E-A1C1-A的大小为 .
.
函数f(x)对任意x∈R都有 .
.
(1)求 和
和 (n∈N*)的值;
(n∈N*)的值;
(2)数列{an}满足: ,求an;
,求an;
(3)令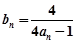 ,
,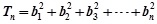 ,
,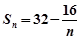 ,试比较Tn和Sn的大小。
,试比较Tn和Sn的大小。
设函数 .
.
(1)求函数f(x)的最大值和最小正周期。
(2)设A、B、C为⊿ABC的三个内角,若 ,
, ,且C为锐角,求
,且C为锐角,求 .
.