如图,在破残的圆形残片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=8cm,CD=2cm.(本小题满分8分)
(1)求作此残片所在的圆(尺规作图,不写作法,保留作图痕迹);
(2)求出(1)中所作圆的半径.
如图所示,将正方形ABCD中的△ABD绕对称中心O旋转至△GEF的位置,EF交AB于M,GF交BD于N.请猜想AM与GN有怎样的数量关系?并证明你的结论.
王老师为学校购买某种篮球,体育用品商店老板给出了如下优惠条件:如果一次性购买不超过10个,单价为80元;如果一次性购买多于10个,那么每增加1个,购买的所有篮球的单价降低2元,但单价不得低于50元.按此优惠条件,王老师一次性购买这种篮球付了1200元.请问王老师购买了多少个这种篮球?
已知关于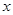 的一元二次方程
的一元二次方程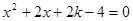 有两个不相等的实数根.
有两个不相等的实数根.
(1)求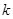 的取值范围;
的取值范围;
(2)若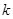 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求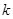 的值.
的值.
已知方程 的一个根是3,求m的值及方程的另一个根.
的一个根是3,求m的值及方程的另一个根.
先化简,再求值:( -1+
-1+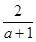 )÷(
)÷(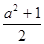 ),其中
),其中 =
= -1.
-1.