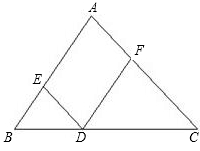
Rt△ABC中,AB=AC=2,∠A=90°,D为BC中点,点E,F分别在AB,AC上,且BE=AF,
(1)求证:ED=FD,
(2)求证:DF⊥DE,
(3)求四边形AFDE的面积.
看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
解:∵∠1=35°,∠2=35°(已知),
∴∠1=∠2
∴_______∥_______(同位角相等,两条直线平行)
又∵AC⊥AE(已知),
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=_______°(等式的性质)
同理可得,∠FBD+∠2=_______°
∴_______∥_______(同位角相等,两条直线平行)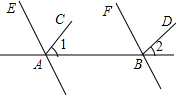
完成下列解答过程:
证明:(1)∵∠A=_______,(已知)
∴AC∥ED.(_______)
(2)∵∠EDF=_______,(已知)
∴AC∥ED.(_______)
(3)∵∠A+∠DFA=180°(已知)
∴_______∥_______.(_______)
如图,已知a∥b,∠3+∠2=180°,b与c平行吗?说明理由.
先作图,再证明.
(1)在所给的图形(如图)中完成下列作图(保留作图痕迹)
①作∠ACB的平分线CD,交AB于点D;
②延长BC到点E,使CE=CA,连接AE;
(2)求证:CD∥AE.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,将△ADC沿AC边所在的直线折叠,使点D落在点E处,得四边形ABCE.
求证:EC∥AB.