看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
解:∵∠1=35°,∠2=35°(已知),
∴∠1=∠2
∴_______∥_______(同位角相等,两条直线平行)
又∵AC⊥AE(已知),
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=_______°(等式的性质)
同理可得,∠FBD+∠2=_______°
∴_______∥_______(同位角相等,两条直线平行)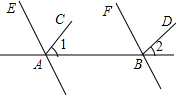
我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.例如,代数式 的几何意义是数轴上 所对应的点与2所对应的点之间的距离:因为 ,所以 的几何意义就是数轴上 所对应的点与 所对应的点之间的距离.
(1)发现问题:代数式 的最小值是多少?
(2)探究问题:如图,点 、 、 分别表示数 、2、 , .

的几何意义是线段 与 的长度之和,
当点 在线段 上时, ,当点 在点 的左侧或点 的右侧时, .
的最小值是3.
(3)解决问题:
① 的最小值是 ;
②利用上述思想方法解不等式: ;

③当 为何值时,代数式 的最小值是2.
甲、乙两家商场平时以同样价格出售相同的商品.新冠疫情期间,为了减少库存,甲、乙两家商场打折促销.甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.
(1)以 (单位:元)表示商品原价, (单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数解析式;
(2)新冠疫情期间如何选择这两家商场去购物更省钱?
某校为了响应市政府号召,在“创文创卫”活动周中,设置了“ :文明礼仪, :环境保护, :卫生保洁, :垃圾分类”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如图条形统计图和扇形统计图.

(1)本次调查的学生人数是 人, ;
(2)请补全条形统计图;
(3)学校要求每位同学从星期一至星期五选择两天参加活动.如果小张同学随机选择连续两天,其中有一天是星期一的概率是 ;小李同学星期五要参加市演讲比赛,他在其余四天中随机选择两天,其中有一天是星期三的概率是 .
如图,在正方形 中,点 在 边的延长线上,点 在 边的延长线上,且 ,连接 和 相交于点 .
求证: .

先化简,再求值: ,其中 是不等式组 的整数解.