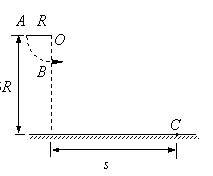
在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为 (单位:
(单位: ),式中
),式中 。将一光滑小环套在该金属杆上,并从
。将一光滑小环套在该金属杆上,并从 处以
处以 的初速度沿杆向下运动,取重力加速度
的初速度沿杆向下运动,取重力加速度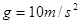 。求
。求
(1)当小环运动到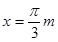 时的速度大小;
时的速度大小;
(2)该小环最远能运动到的什么位置?
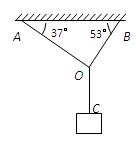
如图所示,轻绳AO、BO所能承受的最大拉力分别为Fm1=132N、Fm2 =160N,轻绳OC能承受足够大拉力。它们一端固定在水平天花板上,在它们的结点O处用的悬吊一重物,绳AO、BO与天花板间的夹角分别为37°和53°。为保证绳均不断裂,重物的质量应不超过多少?
(取g =10m/s2,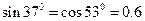 ,
,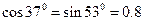 )
)
如图所示,A、B两物体的质量分别为mA、mB,用劲度系数为k的轻弹簧相连,物体B放在水平面上。开始时,A、B都处于静止状态。现对A施加一个竖直向上的力F,缓慢将A提起,直到使B恰好离开地面,求这一过程中,物体A上移的距离。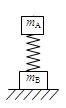
为测定气垫导轨上滑块的加速度,滑块上安装了宽度为d = 0.9cm的遮光板(如图所示)。滑块在牵引力作用下先后通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为△t1 = 0.029s,通过第二个光电门的时间为△t2 = 0.011s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t = 0.76s,求滑块的加速度。(结果保留两位有效数字)

如图所示,在水平地面上放置一块质量为M的长平板B,在平板的上方某一高度处有一质量为m的物块P由静止开始落下。在平板上方附近存在“相互作用”的区域(如图中虚线所示区域),当物块P进入该区域内,B便会对P产生一个竖直向上的恒力f作用,使得P恰好不与B的上表面接触,且f=kmg,其中k=11。在水平方向上P、B之间没有相互作用力。已知平板与地面间的动摩擦因数 ,平板和物块的质量之比M/m=10。在P开始下落时,平板B向左运动的速度v0=1.0m/s,P从开始下落到进入相互作用区域经历的时间t0=2.0s。设平板B足够长,保证物块P总能落到B板上方的相互作用区域内,忽略物块P受到的空气阻力,取重力加速度g=10m/s2。求:
,平板和物块的质量之比M/m=10。在P开始下落时,平板B向左运动的速度v0=1.0m/s,P从开始下落到进入相互作用区域经历的时间t0=2.0s。设平板B足够长,保证物块P总能落到B板上方的相互作用区域内,忽略物块P受到的空气阻力,取重力加速度g=10m/s2。求:
(1)物块P从开始下落到再次回到初始位置所经历的时间。
(2)从物块P开始下落到平板B的运动速度减小为零的这段时间内,P能回到初始位置的次数。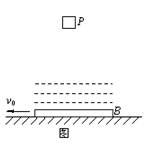
如图所示,一对杂技演员(都视为质点)乘秋千从A点(秋千绳处于水平位置)由静止出发绕O点下摆,当摆到最低点B时,女演员在极短时间内将男演员沿水平方向推出,然后自已刚好能回到高处A。求男演员落地点C与O点的水平距离s。已知男演员质量是女演员质量的2倍,秋千的质量不计,秋千的摆长为R,O点离地面的高度为5R。