如图所示,质量为m=0.1kg粗细均匀的导线,绕制成闭合矩形线框,其中长LAC=50cm,宽LAB=20cm,竖直放置在水平面上。中间有一磁感应强度B=1.0T,磁场宽度d=10cm的匀强磁场。线框在水平向右的恒力F=2N的作用下,由静止开始沿水平方向运动,使AB边进入磁场,从右侧以v=1m/s的速度匀速运动离开磁场,整个过程中始终存在大小恒定的阻力Ff=1N,且线框不发生转动。求线框AB边: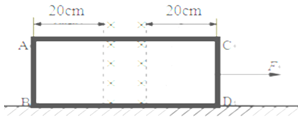
(1)离开磁场时感应电流的大小;
(2)刚进入磁场时感应电动势的大小;
(3)求线框穿越磁场的过程中产生的焦耳热。
如图所示,光滑圆柱半径为R,被固定在水平平台 上,用轻绳跨过圆柱体与两小球m1、m2相连(m1、m2分别为它们的质量),开始时让m1放在平台上,两边绳绷直,两球从静止开始m1上升,m2下降.当m1上升到圆柱的最高点时,球m1对轨道的压力0.2m1g,求:
上,用轻绳跨过圆柱体与两小球m1、m2相连(m1、m2分别为它们的质量),开始时让m1放在平台上,两边绳绷直,两球从静止开始m1上升,m2下降.当m1上升到圆柱的最高点时,球m1对轨道的压力0.2m1g,求:
(1)小球m1上升到圆柱的最高点时,速度多大?(用g、R表示)
(2)两球从静止开始至m1上升到圆柱的最高点,系统减少的势能为多少?
(3)m2应为m1的多少倍?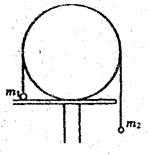
如图,一劲度k=800N/m的轻弹簧两端各焊接着质量均为m=12kg的物体A、B,竖直静止在水平地面上。现要加_竖直向上的力F在上面物体A上,使A开始向上做匀加速运动,经0.4s,B刚要离开地面,整个过程弹簧都处于弹性限度内(g=10m/s)。求此过程所加外力F的最大值和最小值。
如图所示,水平传送带在电劫机的带动下,始终保持v的速度运行。质量为m的工件(可视为质点)轻轻放在传送带上,过一会儿与传送带相对静止。对于这个过程,求:电动机由于传送工件多消耗的电能。
跳伞运动员做低空跳伞表演;他在离地面224m离处,由静止开始在竖直方向做自由落体运动。一段时间后,运动员打开降落伞,以12.5m/s。的加速度匀减速下降 ,为了运动员的安全,要求运动员落地速度最大不得超过5m/s。(g=10m/s)问:
,为了运动员的安全,要求运动员落地速度最大不得超过5m/s。(g=10m/s)问:
(1)运动员展开伞时,离地面高度至少为多少?
(2)运动员在空中的最短时间是多少?
[物理——选修3-5]
(1)以下说法正确的是()
| A.当氢原子从n = 4的状态跃迁到n = 2的状态时,发射出光子 |
| B.光电效应和康普顿效应都揭示了光具有波动性 |
| C.原子核的半衰期与原子所处的化学状态和外部条件有关 |
| D.比结合能越大,原子核中核子结合得越牢固,原子越稳定 |
(2)一长为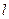 ,质量为M的木板静止在光滑的水平面上,一质量为
,质量为M的木板静止在光滑的水平面上,一质量为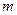 的滑块的初速度
的滑块的初速度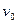 滑到木板上,木板长度至少为多少才能使滑块不滑出木板。(设滑块与木板间动摩擦因数为
滑到木板上,木板长度至少为多少才能使滑块不滑出木板。(设滑块与木板间动摩擦因数为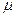 )
)