阅读理解题： 如图，在△ABC中，AD是BC边上的中线，且AD=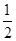
BC．
求证：∠BAC=90°．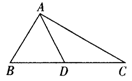
证明：∵AD=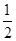BC，BD=CD=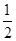BC，
∴AD=BD=DC，
∴ADB和 ADC都是等腰三角形
∴∠B=∠BAD，∠C=∠CAD，
∵∠B+∠BAD+∠CAD+∠C=180°，
∴∠BAD+∠CAD=90°，即∠BAC=90°．
（1）此题实际上是直角三角形的另一个判定方法，请你用文字语言叙述出来．
（2）直接运用这个结论解答题目：一个三角形一边长为2，这边上的中线长为1，另两边之和为1+
，求这个三角形的面积．
【知识储备：勾股定理：在直角三角形中。两直角边的平方和等于斜边的平方。】
的值与x的值无关，求m的值．
；
．
的意义是
．
．
的值．
时，
值．