某自行车厂计划每天平均生产n辆自行车，而实际产量与计划产量相比有出入．下表记录了某周五个工作日每天实际产量情况（超过计划产量记为正、少于计划产量记为负）：
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 实际生产量 |
+5 |
-2 |
-4 |
+13 |
-3 |
（1）用含n的代数式表示本周前三天生产自行车的总数；
（2）该厂实行每日计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，当n=100时，那么该厂工人这一周的工资总额是多少元？
（3）若将上面第（2）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件不变，则这一周工人的工资与按日计件的工资哪一个更多？请说明理由．
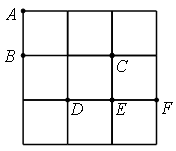
在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.从A、D、E、F四点中任意取一点，以所取的这一点及B、C为顶点三角形，则所画三角形是等腰三角形的概率是▲；
从A、D、E、F四点中先后任意取两个不同的点，以所取的这两点及B、C为顶点画四边形，求所画四边形是平行四边形的概率（用树状图或列表求解）.
我国是一个淡水资源严重缺乏的国家，有关数据显示，中国人均淡水资源占有量仅为美国人均淡水资源占有量的
，中、美两国人均淡水资源占有量之和为13800
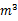，问中、美两国人均淡水资源占有量各为多少（单位：）？
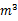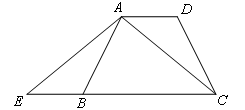
如图，在梯形ABCD中，已知AD∥BC，AB=CD，延长线段CB到E，使BE=AD，连接AE、AC.求证：△ABE≌△CDA；
若∠DAC=40°，求∠EAC的度数.
已知一抛物线经过
（0，0），
（1，1）两点，且解析式的二次项系数为
（
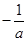
＞0）.当
时，求该抛物线的解析式，并用配方法求出该抛物线的顶点坐标；已知点
（0，1），若抛物线与射线
相交于点
，与
轴相交于点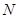
（异于原点），当在什么范围内取值时，
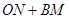的值为常数？当在什么范围内取值时，
的值为常数？若点
（
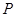，）在抛物线上，则称点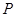为抛物线的不动点.将这条抛物线进行平移，使其只有一个不动点，此时抛物线的顶点是否在直线
上，请说明理由.
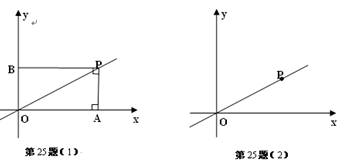
已知点P是直线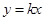
（
＞0，）上一定点，点A是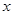
轴上一动点（不与原点重合），连结PA，过点P作PB⊥PA，交
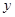轴于点B，探究线段PA与PB 的数量关系.如图（1），当PA⊥
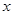轴时，观察图形发现线段PA与PB的数量关系是__________；当PA与
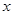轴不垂直时，在图（2）中画出图形，线段PA与PB 的数量关系是否与（Ⅰ）所得结果相同？写出你的猜想并加以证明；为何值时，线段PA=PB？此时∠POA的度数是多少，为什么？