如图，虚线框内为某种电磁缓冲车的结构示意图，其主要部件为缓冲滑块
和质量为
的缓冲车厢．在缓冲车的底板上，沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN．缓冲车的底部，安装电磁铁（图中未画出），能产生垂直于导轨平面的匀强磁场，磁场的磁感应强度为B．导轨内的缓冲滑块由高强度绝缘材料制成，滑块上绕有闭合矩形线圈
，线圈的总电阻为
，匝数为
，
边长为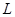
．假设缓冲车以速度
与障碍物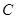
碰撞后，滑块立即停下，此后线圈与轨道的磁场作用力使缓冲车厢减速运动，从而实现缓冲，一切摩擦阻力不计．
（1）求滑块的线圈中最大感应电动势的大小；
（2）若缓冲车厢向前移动距离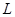后速度为零，缓冲车厢与障碍物和线圈的边均没有接触，则此过程线圈中通过的电量和产生的焦耳热各是多少？
如图所示，宽度为L的金属框架竖直固定在绝缘地面上，框架的上端接有一个压敏电阻元件，其阻值与其两端所加电压成正比，即R=kU，式中k为已知的常数．框架上有一质量为m，离地高为h的金属棒，金属棒与框架始终接触良好无摩擦，且保持水平，磁感应强度为B的匀强磁场，方向垂直于框架平面向里．今将金属棒由静止释放，棒沿框架向下运动，不计金属棒电阻，重力加速度为g．试求：
（1）金属棒运动过程中，流过棒的电流大小和方向；
（2）金属棒落到地面时的速度大小；
（3）金属棒从释放到落地过程中通过电子元件的电量．
如图所示，长为L=6m、质量M=4kg的长木板放置于光滑的水平面上，其左端有一大小可忽略，质量为m=1kg的物块，物块与木板间的动摩擦因数为0.4，开始时物块与木板都处于静止状态，现对物块施加F=8N，方向水平向右的恒定拉力，设最大静摩擦力等于滑动摩擦力。求：（g取10m/s2）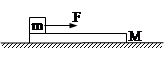
（1）小物块的加速度；
（2）物块从木板左端运动到右端经历的时间。
如图所示，一小滑块静止在倾角为370的斜面底端，滑块受到外力冲击后，获得一个沿斜面向上的速度v0=4m/s，斜面足够长，滑块与斜面之间的动摩擦因数为μ=0.25，已知sin370=0.60，cos370=0.80，g取10m/s2，求：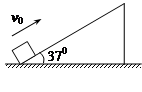
（1）滑块沿斜面上滑过程中的加速度的大小；
（2）滑块沿斜面上滑的最大距离；
（3）滑块返回斜面底端时速度的大小。
水平传送带以v0=4m/s的速度在水平方向做匀速直线运动，这时将一质量为m=1kg的小物体轻轻放在传送带的左端（如图所示），已知传送带与物体的摩擦因数为μ=0.4，传送带的长度为L=6m，问经多长时间能将物体送到右端。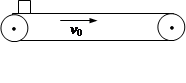
如图所示，直角坐标系位于竖直平面内，在水平的x轴下方存在匀强磁场和匀强电场，磁场的方向垂直xOy平面向外，电场线方向平行于y轴。一质量为m.电荷量为q的带正电的小球，从y轴上的A点以水平速度v0向右抛出，与x轴成450角经x轴上M点进入电场和磁场，恰能做匀速圆周运动，从坐标系原点第一次离开电场和磁场。不计空气阻力，重力加速度为g。求：
（1）电场强度E的大小和方向；
（2）磁感应强度的大小；
（3）求小球从A运动到O的总时间。