(本题8分)已知:抛物线Y=ax2+bx+c经过A(1,0)、B(-3,0)、C(0,3)三点。
求:(1)抛物线的表达式;
(2)写出此抛物线向左平移3个单位,再向下平移2个单位后的抛物线解析式.
解不等式组 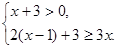 ,并判断
,并判断 是否该不等式组的解.
是否该不等式组的解.
探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:_______________________________.
教材第66页探索平方差公式时设置了如下情境:边长为b的小正方形纸片放置在边长为a的大正方形纸片上(如图9−6),你能通过计算未盖住部分的面积得到公式(a + b) (a−b) = a2−b2吗?(不必证明)
(1)如果将小正方形的一边延长(如图①),是否也能推导公式?请完成证明.
(2) 面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”.例如,著名的赵爽弦图(如图②,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2,也可以表示为4´ ab + (a −b)2,由此推导出重要的勾股定理:a2 + b2 = c2.图③为美国第二十任总统伽菲尔德的“总统证法”,请你完成证明.
ab + (a −b)2,由此推导出重要的勾股定理:a2 + b2 = c2.图③为美国第二十任总统伽菲尔德的“总统证法”,请你完成证明.
(3) 试构造一个图形,使它的面积能够解释(a− 2b)2 = a2−4ab + 4b2,画在下面的格点中,并标出字母a、b所表示的线段.
小玲只画了下图就得出“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等”这个论断,你是否认同小玲的观点?如果认同,则给出证明;如果不认同,则画出所有可能的情况,猜想相应的结论,并给出证明.
我们学习了因式分解之后可以解某些高次方程.例如,一元二次方程x2 + x −2 = 0可以通过因式分解化为:(x −1) (x + 2) = 0,则方程的两个解为x = 1和x = −2.反之,如果x = 1是某方程ax2 + bx + c = 0的一个解,则多项式ax2 + bx + c必有一个因式是(x −1).
在理解上文的基础上,试找出多项式x3 + x2 −3x + 1的一个因式,并将这个多项式因式分解.