(本题12分)某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完.该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售量x(千件)的关系为:
y1=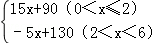
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为
(1)用x的代数式表示t为:t= ;当0<x≤4时,y2与x的函数关系为:y2= ;当 <x< 时,y2=100;
(2)当该公司在国内销售量是国外销量的两倍时,问总利润是多少?
(3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少?
(本题12分)潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
| 种植户 |
种植A类蔬菜面积 (单位:亩) |
种植B类蔬菜面积 (单位:亩) |
总收入 (单位:元) |
| 甲 |
3 |
1 |
12500 |
| 乙 |
2 |
3 |
16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
(本题12分)国家环保局统一规定,空气质量分为5级:当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题: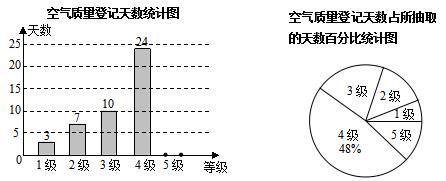
(1)本次调查共抽取了 天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为 °;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
(本题5分)五子棋深受广大棋友的喜爱.规则是:10×10的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上首先连成五颗者为胜.如图是小张和小王的对弈图(小张执黑子先行,小王执白子后走).
观察棋盘思考:若A点的位置记作(8,4),小张必须在哪个位置上落子才不会让小王在短时间内获胜?为什么?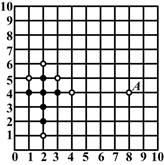
(本题6分)如图,点O在直线AB上,OC平分∠DOB.若∠COB=36°. 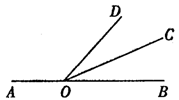
(1)求∠DOB的大小;
(2)请你用量角器先画∠AOD的角平分线OE,再说明OE和OC的位置关系.
(本题共10分,每小题5分)
(1)
(2)