(本题6分)如图,点O在直线AB上,OC平分∠DOB.若∠COB=36°. 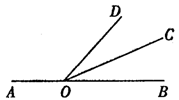
(1)求∠DOB的大小;
(2)请你用量角器先画∠AOD的角平分线OE,再说明OE和OC的位置关系.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.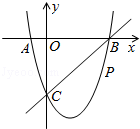
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长在(单位:cm)在5~50之间.每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)有基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的.浮动价与薄板的边长成正比例.在营销过程中得到了表格中的数据.
| 薄板的边长(cm) |
20 |
30 |
| 出厂价(元/张) |
50 |
70 |
(1)求一张薄板的出厂价与边长之间满足的函数关系式;
(2)已知出厂一张边长为40cm的薄板,获得的利润为26元(利润=出厂价﹣成本价),
①求一张薄板的利润与边长之间满足的函数关系式.
②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?
参考公式:抛物线:y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ,
, )
)
如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.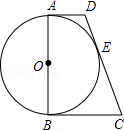
(1)求证:BC为⊙O的切线;
(2)若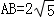 ,AD=2,求线段BC的长.
,AD=2,求线段BC的长.
箱子里有3个红球和2个黄球,从箱子中一次拿两个球出来.
(1)请你用列举法(树形图或列表)求一次拿出的两个球中时一红一黄的概率;
(2)往箱子中再加入x个白球,从箱子里一次拿出的两个球,多次实验统计如下
取出两个球的次数 20 30 50 100 150 200 400
至少有一个球是白球的次数 13 20 35 71 107 146 288
至少有一个球是白球的频率 0.65 0.67 0.70 0.71 0.713 0.73 0.72
请你估计至少有一个球是白球的概率是多少?
(3)在(2)的条件下求x的值.( =0.7222222…)
=0.7222222…)