先阅读下面例题的解题过程,再解答后面的题目。
例:已知代数式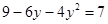 ,求
,求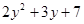 的值。
的值。
解:由 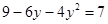 得
得 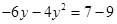 即
即 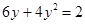
因此 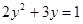 , 所以
, 所以 
题目:已知代数式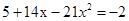 ,求
,求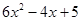 的值。
的值。
如图所示是甲、乙两人追赶过程中路程和时间之间的函数关系图象,由图象回答下列问题:
(1)谁追赶谁?甲、乙两人谁出发早?早几小时?
(2)甲出发几小时后两人相遇?此时他们走了多远?
下面的图象反映的过程是:
张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y表示张强离家的距离.
根据图象回答下列问题:
(1)体育场离张强家_____千米;
(2)体育场离文具店_____千米,张强在文具店停留了_____分;
(3)请计算:张强从文具店回家的平均速度是多少?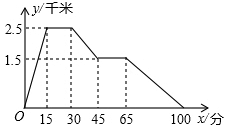
某人沿一条直路行走,此人离出发地的距离S(千米)与行走时间t(分钟)的函数关系如图所示,请根据图象提供的信息回答下列问题:
(1)此人离开出发地最远距离是_____千米;
(2)此人在这次行走过程中,停留所用的时间为_____分钟;
(3)由图中线段OA可知,此人在这段时间内行走的速度是每小时_____千米;
(4)此人在120分钟内共走了_____千米.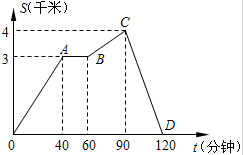
一游泳池长90米,甲、乙两人分别在游泳池相对两边同时朝另一边游泳,图中实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图象,若不计转向时间,请回答下列问题:
(1)甲、乙游泳的平均速度各是多少?
(2)从开始到3分钟之间他们相遇了几次?
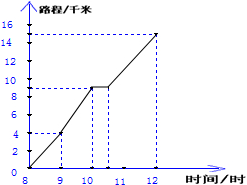
如图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图回答问题:
(1)9时,10时30分,12时所走的路程分别是多少?
(2)他休息了多长时间?
(3)他从休息后直至到达目的地这段时间的平均速度是多少?