如图所示是甲、乙两人追赶过程中路程和时间之间的函数关系图象，由图象回答下列问题：
（1）谁追赶谁？甲、乙两人谁出发早？早几小时？
（2）甲出发几小时后两人相遇？此时他们走了多远？
完成下面的证明：已知，如图，AB∥CD∥GH，EG平分∠BEF，FG平分∠EFD，求证：∠EGF=90°．
证明：∵HG∥AB（已知）
∴∠1=∠3（）
又∵HG∥CD（已知）
∴∠2=∠4（）
∵AB∥CD（已知）
∴∠BEF+___________=180°（）
又∵EG平分∠BEF（已知）
∴∠1=
∠_____________（）
又∵FG平分∠EFD（已知）
∴∠2=
∠_____________（）
∴∠1+∠2=（___________+______________）
∴∠1+∠2=90°， ∴∠3+∠4=90°（）
即∠EGF=90．
已知：如图∠1=∠2，∠C=∠D，那么∠A，∠F相等吗？试说明理由．
如图，在□ABCD中，F是AD的中点，延长BC到点E，使CE=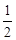
BC，连结DE，CF．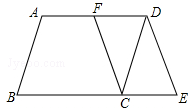
（1）求证：四边形CEDF是平行四边形；
（2）若AB=4，AD=6，∠B=60°，求DE的长．
如图所示，在□ABCD中，对角线AC与BD相交于点O，过点O任作一条直线分别交AB，CD于点E，F．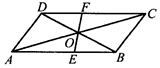
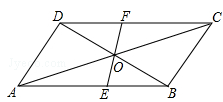
（1）求证：OE=OF；
（2）若AB=7，BC=5，OE=2，求四边形BCFE的周长．
如图所示的一块地，AD=9m，CD=12m，∠ADC=90°，AB=39m，BC=36m，求这块地的面积．