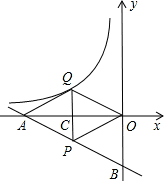
如图,一次函数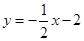 的图象分别交
的图象分别交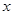 轴、
轴、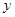 轴于
轴于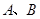 两点,
两点, 为
为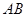 的中点,
的中点,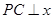 轴于点
轴于点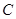 ,延长
,延长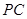 交反比例函数
交反比例函数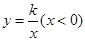 的图象于点
的图象于点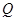 ,且
,且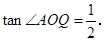
(1)求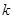 的值;
的值;
(2)连结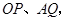 求证:四边形
求证:四边形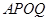 是菱形.
是菱形.
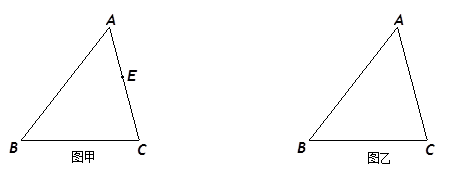
、(本题12分)如图甲,在△ABC中,E是AC边上的一点,
(1)在图甲中,作出以BE为对角线的平行四边形BDEF,使D、F分别在BC和AB边上;
(2)改变点E的位置,则图甲中所作的平行四边形BDEF有没有可能为菱形?若有,请在图乙中作出点E的位置(用尺规作图,并保留作图痕迹);若没有,请说明理由.
 |
(本题12分)某校积极开展每天锻炼1小时活动,老师对本校八年级学生进行一分钟跳绳测试,并对跳绳次数进行统计,绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中,组中值为190次一组的频率为0.12.(说明: 组中值为190次的组别为 180≤次数<200)
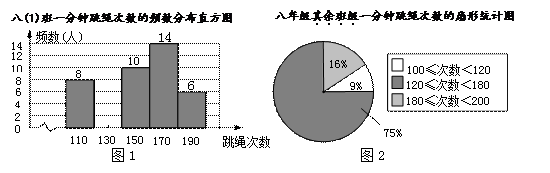 |
请结合统计图完成下列问题:
(1)八(1)班的人数是,组中值为110次一组的频率为;
(2)请把频数分布直方图补充完整;
(3)如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%,那么八年级同学至少有多少人?
(本题10分)如图,双曲线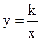 上点A的坐标为(1,2),过点A的直线y=x+b交x轴于点M,交y轴于点N,过A作AP⊥x轴于点P。
上点A的坐标为(1,2),过点A的直线y=x+b交x轴于点M,交y轴于点N,过A作AP⊥x轴于点P。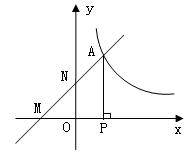
(1)分别求k、b的值;
(2)求△AMP的周长。
(本题8分)如图,△ABC中,已知BE⊥AD,CF⊥AD,且BE=CF.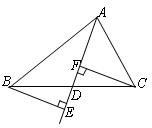
(1)请你判断AD是△ABC的中线还是角平分线?请证明你的结论.
(2)连接BF、CE,若四边形BFCE是菱形,则△ABC中应添加一个条件。
(填上你认为正确的一个条件即可)
(本题8分)2010年上海世博会某展览馆展厅东面有两个入口A,B,南面、西面、北面各有一个出口,示意图如图所示.小华任选一个入口进入展览大厅,参观结束后任选一个出口离开. (1)她从进入到离开共有多少种可能的结果?(要求画出树状图)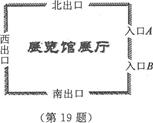
(2)她从入口A进入展厅并从北出口或西出口离开的概率是多少?