如图1,在平面直角坐标系中,抛物线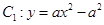 (
(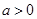 )经过点
)经过点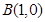 ,顶点为
,顶点为 .
.
(1)求抛物线 的解析式;
的解析式;
(2)如图2,先将抛物线 向上平移使其顶点在原点
向上平移使其顶点在原点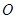 ,再将其顶点沿直线
,再将其顶点沿直线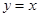 平移得到抛物线
平移得到抛物线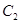 ,设抛物线
,设抛物线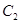 与直线
与直线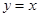 交于
交于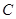 、
、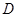 两点,求线段
两点,求线段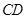 的长.
的长.
(3)在图1中将抛物线 绕点
绕点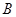 旋转
旋转 后得到抛物线
后得到抛物线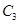 ,直线
,直线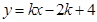 总经过一个定点
总经过一个定点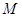 ,若过定点
,若过定点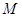 的直线
的直线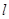 与抛物线
与抛物线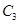 只有一个公共点,求直线
只有一个公共点,求直线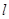 的解析式.
的解析式.
(本小题满分9分)根据要求,解答下列问题.
(1)解下列方程组(直接写出方程组的解即可):
①
 .
.
②
 .
.
③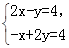
 .
.
(2)以上每个方程组的解中,x值与y值的大小关系为.
(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.
(本小题满分8分)化简: .
.
某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图.
依据图中信息,得出下列结论:
(1)接受这次调查的家长人数为200人;
(2)在扇形统计图中,“不赞同”的家长部分所对应的扇形圆心角大小为162°;
(3)表示“无所谓”的家长人数为40人;
(4)随机抽查一名接受调查的家长,恰好抽到“很赞同”的家长的概率是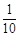 .
.
其中正确的结论个数为()
| A.4 | B.3 | C.2 | D.1 |
我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c= 时,a=,b=.
时,a=,b=.
如图2,当∠ABE=30°,c=4时,a=,b=.
归纳证明
(2)请你观察(1)中的计算结果,猜想 ,
, ,
, 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
拓展应用
(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD= ,AB=3,求AF的长.
,AB=3,求AF的长.
如图,已知二次函数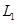 :
: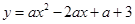 (
(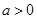 )和二次函数
)和二次函数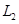 :
: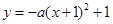 (
(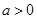 )图象的顶点分别为M,N,与y轴分别交于点E,F.
)图象的顶点分别为M,N,与y轴分别交于点E,F.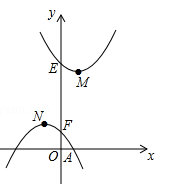
(1)函数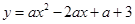 (
(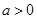 )的最小值为,当二次函数
)的最小值为,当二次函数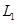 ,
,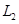 的y值同时随着x的增大而减小时,x的取值范围是;
的y值同时随着x的增大而减小时,x的取值范围是;
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明);
(3)若二次函数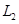 的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程
的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程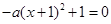 的解.
的解.