在一次数学测验活动中,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直)。如示意图,当小明移动到D点时,眼睛C与铅笔、旗杆的顶端M、A共线,同时,眼睛C与它们的底端N、B也恰好共线。此时,测得DB=50m,小明的眼睛C到铅笔的距离为0.65m,铅笔MN的长为0.16m,请你帮助小明计算出旗杆AB的高度(结果精确到0.1m)。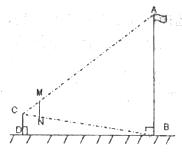
如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.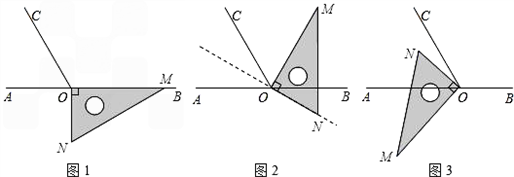
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM -∠NOC的度数.
两种移动电话计费方式表如下:
| 全球通 |
神州行 |
|
| 月租费 |
15元/月 |
0 |
| 本地通话费 |
0.10元/分 |
0.20元/分 |
(1)一个月内某用户在本地通话时间为x分钟,请你用含有x的式子分别写出两种计费方式下该用户应该支付的费用;
(2)若某用户一个月内本地通话时间为5个小时,你认为采用哪种方式较为合算?
(3)小王想了解一下一个月内本地通话时间为多少时,两种计费方式的收费一样多.请你帮助他解决一下.
如图,四边形ABCD与四边形CEFG是两个边长分别为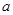 、
、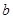 的正方形.
的正方形.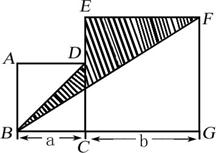
(1)用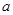 、
、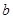 的代数式表示三角形BGF的面积;
的代数式表示三角形BGF的面积;
(2)当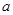 =4cm,
=4cm,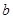 =6cm时,求阴影部分的面积.
=6cm时,求阴影部分的面积.
请在下列括号内填上合适的理由:
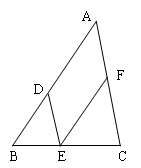
如图,已知DE//AC,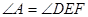 ,试说明
,试说明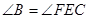 .
.
证明:∵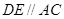 (已知)
(已知)
∴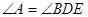 ()
()
∵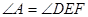 (已知)
(已知)
∴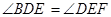 (等量代换)
(等量代换)
∴ ()
()
∴ ()
()
如图, ,直线
,直线 分别与
分别与 交于点
交于点 ,GM⊥EF,HN⊥EF,交AB于点N,
,GM⊥EF,HN⊥EF,交AB于点N,
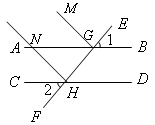
(1)求 的度数;
的度数;
(2)试说明HN∥GM;
(3) °.
°.