两种移动电话计费方式表如下:
| |
全球通 |
神州行 |
| 月租费 |
15元/月 |
0 |
| 本地通话费 |
0.10元/分 |
0.20元/分 |
(1)一个月内某用户在本地通话时间为x分钟,请你用含有x的式子分别写出两种计费方式下该用户应该支付的费用;
(2)若某用户一个月内本地通话时间为5个小时,你认为采用哪种方式较为合算?
(3)小王想了解一下一个月内本地通话时间为多少时,两种计费方式的收费一样多.请你帮助他解决一下.
某房地产开发公司计划建A、B两种户型的住房共80套,已知该公司所筹集的资金不少于2090万元,但不超过2096万元,且所筹集资金全部用于建房,两种户型的建房成本和售价如下表:
| 户型 |
A |
B |
| 成本(万元/套) |
25 |
28 |
| 售价(万元/套) |
30 |
34 |
(1)试求该公司对这两种户型住房将有哪几种建房方案;
(2)试问该公司将如何建房,才能使获得的利润最大;
(3)若根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(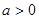 ),且所建的两种住房可全部售出.试问该公司又将如何建房,才能使获得的利润最大。(注:利润=售价-成本)
),且所建的两种住房可全部售出.试问该公司又将如何建房,才能使获得的利润最大。(注:利润=售价-成本)
阅读下列材料,然后解答后面的问题。
我们知道方程 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由 ,得
,得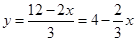 ,(
,( 、
、 为正整数)
为正整数) 则有
则有 .
.
又 为正整数,则
为正整数,则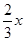 为正整数.
为正整数.
由2与3互质,可知: 为3的倍数,从而
为3的倍数,从而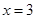 ,代入
,代入 .
. 的正整数解为
的正整数解为
问题:(1)请你写出方程 的一组正整数解:
的一组正整数解:
(2)若 为自然数,则满足条件的
为自然数,则满足条件的 值有个
值有个
| A.2 | B.3 | C.4 | D.5 |
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
用8块相同的长方形地砖拼成一块长方形地面,地砖的拼放方式及相关数据如图所示,求这块长方形地面的面积。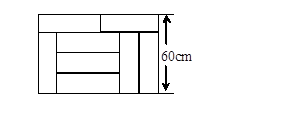
今年春节,小强到爷爷家拜年,爷爷说过年了,大家都长了一岁,小强问爷爷多大岁了。爷爷说:“我现在的年龄是你年龄的5倍,再过12年,我的年龄是你年龄的3倍,你算算我现在的年龄是多少?”聪明的同学,请你帮帮小强,算出爷爷的岁数。
已知关于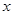 、
、 的方程组
的方程组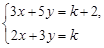 的解满足
的解满足 ,求
,求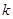 的取值范围。
的取值范围。