某房地产开发公司计划建A、B两种户型的住房共80套，已知该公司所筹集的资金不少于2090万元，但不超过2096万元，且所筹集资金全部用于建房，两种户型的建房成本和售价如下表：
| 户型 |
A |
B |
| 成本（万元/套） |
25 |
28 |
| 售价（万元/套） |
30 |
34 |
（1）试求该公司对这两种户型住房将有哪几种建房方案；
（2）试问该公司将如何建房，才能使获得的利润最大；
（3）若根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元（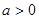
），且所建的两种住房可全部售出．试问该公司又将如何建房，才能使获得的利润最大。（注：利润=售价－成本）
如图，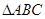
三个顶点坐标分别为
，
，
．
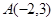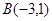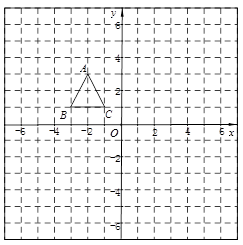
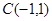（1）请画出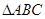关于
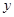轴对称的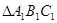
；
（2）以原点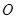
为位似中心，将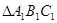放大为原来的2倍，得到
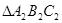，请在第三象限内画出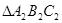，并求出
：
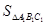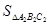的值．
解方程：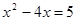
．
先化简，再求值: 
，其中
.
在平面直角坐标系xOy中，抛物线
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C（0,4），D为OC的中点.
（1）求m的值；
（2）抛物线的对称轴与 x轴交于点E，在直线AD上是否存在点F，使得以点A、B、F为顶点的三角形与△ADE 相似？若存在，请求出点F的坐标，若不存在，请说明理由；
（3）在抛物线的对称轴上是否存在点G，使△GBC中BC边上的高为
？若存在，求出点G的坐标；若不存在请说明理由．
已知△ABC和△ADE是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE中点，连结DF、CF.
（1）如图1,当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；
（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；
（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD=1，AC=
，求此时线段CF的长(直接写出结果).