(·湖南常德)如图,曲线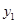 抛物线的一部分,且表达式为:
抛物线的一部分,且表达式为: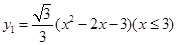 曲线
曲线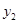 与曲线
与曲线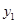 关于直线
关于直线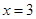 对称。
对称。
(1)求A、B、C三点的坐标和曲线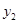 的表达式;
的表达式;
(2)过点D作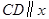 轴交曲线
轴交曲线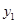 于点D,连接AD,在曲线
于点D,连接AD,在曲线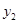 上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标。
上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标。
(3)设直线CM与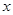 轴交于点N,试问在线段MN下方的曲线
轴交于点N,试问在线段MN下方的曲线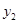 上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由。
上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由。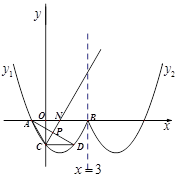
(本小题满分5分)已知:如图,在 中,
中,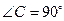 ,点
,点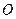 在
在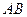 上,以
上,以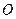 为圆心,
为圆心,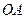 长为半径的圆与
长为半径的圆与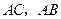 分别交于点
分别交于点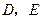 ,且
,且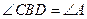 .
.
(1)判断直线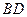 与
与 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若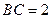 ,
,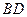 =
=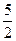 ,求
,求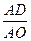 的值.
的值.
(本小题满分5分)在△ABC中,AB=AC,∠BAC=1 20°,过点C
20°,过点C 作CD∥AB,且CD=2AB,联结BD,BD=2.求△ABC的面积.
作CD∥AB,且CD=2AB,联结BD,BD=2.求△ABC的面积.
(本小题满分5分)已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
(1)求反比例函数与二次函数的解析式;
(2)设二次函数图象的顶点为B,判断点B是否在反比例函数的图象上,并说明理由;
|
(3)若反比例函数图象上有一点P,点P的横坐标为1,求△AOP的面积.
(本小题满分5分)列方程或方程组解应用题:
九年级(1)班的学生周末乘汽车到游览区游览,游览区到学校120千米,一部分学生乘慢车先行,出发1小时后,另一部分学生乘快车前往,结果他们同时到达,已知快车速度是慢车速度的1.5倍,求慢车的速度.
(本小题满分5分)已知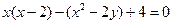 ,求代数式
,求代数式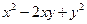 的值.
的值.