(本小题满分12分)正方体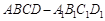 的棱长为l,点F、H分别为A1D、A1C的中点.
的棱长为l,点F、H分别为A1D、A1C的中点.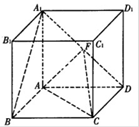
(1)证明:A1B∥平面AFC;
(2)证明:B1H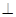 平面AFC.
平面AFC.
已知数列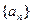 是首项为1的等差数列,且公差不为零,而等比数列
是首项为1的等差数列,且公差不为零,而等比数列 的前三项分别是
的前三项分别是 。
。
(1)求数列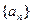 的通项公式
的通项公式
(2) )若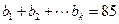 ,求正整数
,求正整数 的值。
的值。
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos=,·=3.
(1)求△ABC的面积;
(2)若c=1,求a的 值.
值.
已知|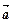 |=,|
|=,|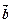 |=2.
|=2.
(1)若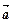 与
与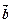 的夹角为150°,求|
的夹角为150°,求|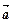 +2
+2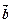 |;
|;
(2)若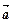 -
-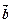 与
与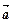 垂直,求
垂直,求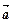 与
与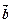 的夹角大小.
的夹角大小.
在△ABC中,角A、B、C所对应的边分别为a,b,c,已知a=3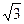 ,c=2,B=150°,求边b的长及A的正弦值.
,c=2,B=150°,求边b的长及A的正弦值.
(本小题10分)
对于函数f(x)(x )恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
)恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
(1)求f(4)、f(1)、f(-1)的值;
(2)求证f(x)为偶函数;
(3)求证f(x)在(0,+ )上是增函数;
)上是增函数;
(4)解不等式f(x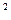 -5)<2.
-5)<2.