某市政府欲在如图所示的矩形
的非农业用地中规划出一个休闲娱乐公园（如图中阴影部分），形状为直角梯形
（线段
和
为两条底边），已知
，
，
，其中曲线
是以
为顶点、
为对称轴的抛物线的一部分．
（1）以为原点，
所在直线为
轴建立直角坐标系，求曲线所在抛物线的方程；
（2）求该公园的最大面积．
为确保信息安全，信息需加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知加密规则如图所示，例如，明文1，2，3，4对应密文5，7，18，16． 当接收方收到密文14，9，23，28时，则解密得到的明文为．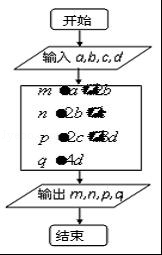
为了保证信息安全传输，设计一种密码系统，其加密、解密原理如下图：
现在加密方式为：把发送的数字信息X，写为“a11a21a12a22”的形式，先左乘矩阵A=
，再左乘矩阵B=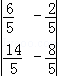
，得到密文Y，现在已知接收方得到的密文4，12，36，72，试破解该密码．
证明：对任给的奇素数p，总存在无穷多个正整数n使得p|（n2n﹣1）．
已知简单多面体的顶点数、面数、棱数分别为V、F、E，多面体的各面为正x边形，过同一顶点的面数为y．求证：
+
﹣
=
．
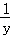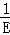下面（a）（b）（c）（d）为四个平面图：
（1）数出每个平面图的顶点数、边数、区域数（不包括图形外面的无限区域），并将相应结果填入表：
| 顶点数 |
边数 |
区域数 |
|
| （a） |
4 |
6 |
3 |
| （b） |
12 |
||
| （c） |
6 |
||
| （d） |
15 |
（2）观察表，若记一个平面图的顶点数、边数、区域数分别为E、F、G，试推断E、F、G之间的等量关系；
（3）现已知某个平面图有2009个顶点，且围成2009个区域，试根据以上关系确定该平面图的边数．