如图所示,甲带电体固定在绝缘水平面上的O点.另一个电荷量为+q、质量为m的带电体乙,从P点由静止释放,经L运动到Q点时达到最大速度v.已知乙与水平面的动摩擦因数为μ,静电力常量为k. 求: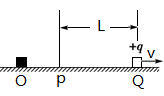
(1)Q处电场强度的大小
(2)P、Q两点电势差
a、b两物体从同一位置沿同一直线运动,它们的速度图象如图所示,求在60s末,a在b前方还是后方,相距多远? 
在一直线的宽公路上,某车以2m/s2的加速度由静止启动,当加速到24m/s时,立即停止加速,同时以6m/s2的加速度刹车,试求此车在13s末及18s末的速度。
汽车以36km/h的速度匀速行驶10s,然后又以1.5m/s2的加速度匀加速行驶10s。
求:(1)汽车在15s末的瞬时速度;
(2)求出汽车在20s内的位移;
(3)汽车在20s内的平均速度。
让小球从斜面的顶端滚下(如图所示标出了不同时刻小球沿斜面滚下的位置),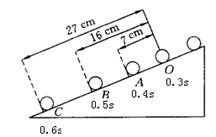
求:(1)粗略计算小球在A点和B点的瞬时速度;
(2)小球运动的加速度。
一架飞机水平匀速地在某位同学头顶飞过,当他听到飞机的发动机声从头顶正上方传来时,发现飞机在他前上方约与地面成60°角的方向上,据此可估算出此飞机的速度约为声速的多少倍?