如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,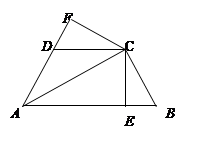
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,AC=17,求CF的长.
如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC. 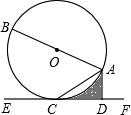
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=300,求图中阴影部分的面积.
如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=900,∠BCO=450,BC=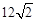 ,点C的坐标为(-18,0).
,点C的坐标为(-18,0).
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的解析式.
交通安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据: );
);
(2)已知本路段对汽车限速为40千米/小时,若测得某辆汽车从A到B用时为2秒,这辆汽车是否超速?说明理由.
“六•一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
| 类别 |
儿童玩具 |
童车 |
童装 |
| 抽查件数 |
90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.

(1)在图1中画出△ABC,使△ABC为直角三角形(点C在小正方形的顶点上,画出一个即可);
(2)在图2中画出△ABD,使△ABD为等腰三角形(点D在小正方形的顶点上,画出一个即可).