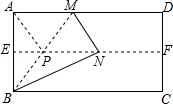
已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.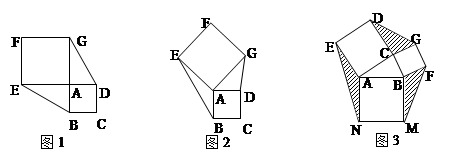
(1)发现:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积
关系是: .
(2)引申:当正方形AEFG旋转任意一个角度时(如图2),△ABE与△ADG的面
积关系是:______________________.并证明你的结论.
证明:
(3)运用:已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图3),则图中阴影部分的面积和的最大值是 cm2.
用指定的方法解下列方程:
(1)x2+4x﹣1=0(用配方法);
(2)2x2﹣8x+3=0(用公式法).
如图,已知抛物线y=ax2+bx﹣4与x轴交于A(﹣2,0),B(8,0)两点,与y轴交于点C,连接BC,以BC为一边,作菱形BDEC,使其对角线在坐标轴上,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求抛物线的解析式;
(2)将抛物线向上平移n个单位,使其顶点在菱形BDEC内(不含菱形的边),求n的取值范围;
(3)当点P在线段OB上运动时,直线l交BD于点M.试探究m为何值时,四边形CQMD是平行四边形,并说明理由.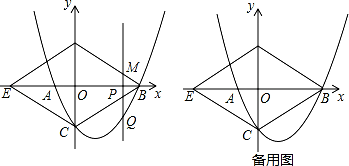
如图,已知正方形ABCD,AC、BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.
(1)若点E在图1的位置,判断OE与OF的数量关系,并证明你的结论;
(2)若点E在AC的延长线上,请在图2中按题目要求补全图形,判断OE与OF的数量关系,并证明你的结论.
已知关于x的方程mx2﹣3(m+1)x+2m+3=0.
(1)求证:无论m取任何实数,该方程总有实数根;
(2)若m≠0,抛物线y=mx2﹣3(m+1)x+2m+3与x轴的交点到原点的距离小于2,且交点的横坐标是整数,求m的整数值.
【问题提出】如果我们身边没有量角器和三角板,如何作15°大小的角呢?
【实践操作】如图.
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开,得到AD∥EF∥BC.
第二步:再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM.折痕BM 与折痕EF相交于点P.连接线段BN,PA,得到PA=PB=PN.
【问题解决】
(1)求∠NBC的度数;
(2)通过以上折纸操作,还得到了哪些不同角度的角?请你至少再写出两个(除∠NBC的度数以外).
(3)你能继续折出15°大小的角了吗?说说你是怎么做的.