已知关于x的一元二次方程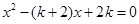 .
.
(1)试说明无论 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根;
(2)若等腰△ABC的一边长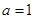 ,另两边长
,另两边长 、
、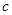 恰好是这个方程的两个根 ,求△ABC的周长.
恰好是这个方程的两个根 ,求△ABC的周长.
如图,抛物线y= x2-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
x2-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
(1)直接写出A、B、C的坐标;
(2)求抛物线y= x2-x-4的对称轴和顶点坐标;
x2-x-4的对称轴和顶点坐标;
(3)求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ,求DE的长.
,求DE的长.
如图,已知正比例函数y= x与反比例函数y=
x与反比例函数y= (k>0)的图象交于A、B两点,且点A的横坐标为4.
(k>0)的图象交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y= (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中各调查一个班级,根据相关数据,绘制如下统计图.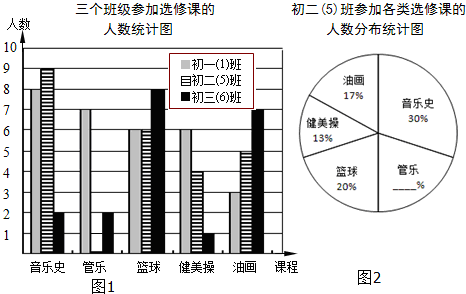
(1)请根据以上信息,直接补全条形统计图(图1)和扇形统计图(图2);
(2)若初一年级有180人,请估算初一年级中有多少学生选修音乐史?
(3)若该校共有学生540人,请估算全校有多少学生选修篮球课?
如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.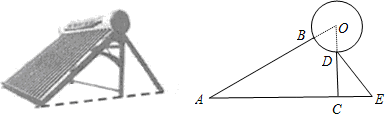
(1)求垂直支架CD的长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果保留三个有效数字,参考数据: ≈1.414,
≈1.414,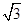 ≈1.73)
≈1.73)