如图,在平面直角系中,点A、B分别在x轴、y轴上,A(8,0),B(0,6),点P从点B出发,沿BA以每秒1个单位的速度向点A运动,点Q从点A出发,沿AO以每秒1个单位的速度向点O运动,当点Q到达点O时,两点同时停止运动,设点Q的运动时间为t秒.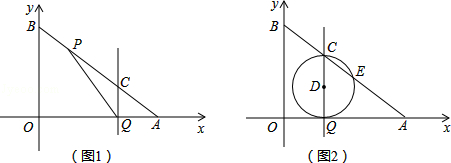
(1)用含t的代数式表示C点坐标;
(2)如图1,连接PQ,过点Q作QC⊥AO交AB于点C,在整个运动过程中,当t为何值时,△CPQ为等腰三角形?
(3)如图2,以QC为直径作⊙D,⊙D与AB的另一个公共点为E.问是否存在某一时刻t,使得以BC、CE、AE的长为边的三角形为直角三角形?若存在,直接写出一个符合题意的t的值;若不存在,请说明理由.
某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(100﹣x)件.设这段时间内售出该商品的利润为y元.
(1)直接写出利润y与售价x之间的函数关系式;
(2)当售价为多少元时,利润可达1000元;
(3)应如何定价才能使利润最大?
如图,某建筑物的截面可以视作由两条线段AB,BC和一条曲线围成的封闭的平面图形.已知AB⊥BC,曲线是以点D为顶点的抛物线的一部分,BC=6m,点D到BC,AB的距离分别为4m和2m.
(1)请以BC所在直线为x轴(射线BC的方向为正方向),AB所在直线为y轴建立平面直角坐标系,求出抛物线的解析式,并直接写出自变量的取值范围;
(2)求AB的长.
如图,E是正方形ABCD中CD边上任意一点.
(1)以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形;
(2)在BC边上画一点F,使△CFE的周长等于正方形ABCD的周长的一半,请简要说明你取该点的理由.
如图,在⊙O中,半径OA⊥弦BC,点E为垂足,点D在优弧上.
(1)若∠AOB=56°,求∠ADC的度数;
(2)若BC=6,AE=1,求⊙O的半径.
不透明的袋子中装有红色小球1个、绿色小球2个,除颜色外无其他差别.
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画村状图的方法求出“两球都是绿色”的概率;
(2)随机摸出两个小球,直接写出两次都是绿球的概率.