如图甲所示,质量m=1kg的物体沿倾角θ=37o的固定粗糙斜面由静止开始向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k表示,物体加速度a与风速v的关系如图乙所示。求:(设风力与物块的运动速度无关)(sin370=0.6, cos370=0.8, g=10m/s2)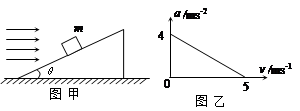
(1)物体与斜面间的动摩擦因数
(2)比例系数k
两平行板间有水平匀强电场,一根长为L=0.1m,不可伸长的不导电细绳的一端连着一个质量为 m=0.1g、带电量为q=5x10-6C的小球,另一端固定于O点.把小球拉起直至细线与电场线平行,然后无初速度释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ=37°求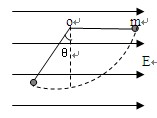
(1) 匀强电场的场强大小
(2)经过最低点时,小球对细线的拉力.
如图所示,四分之一圆轨道OA与水平轨道AB相切,它们与另一水平轨道CD在同一竖直面内,C点在B点的正下方,C、D两点间的距离为X=8m;圆轨道OA的半径R=0.2 m,OA与AB均光滑,一质量m=1 kg的滑块从O点由静止释放,当滑块经过B点时,一小车由D点以初速度v0 =3m/s向C点做匀减速运动直到静止,加速度大小a=1 m/s2,运动一段时间后滑块恰好落入小车中.(取g=10 m/s2)求: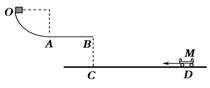
(1)滑块滑经A点时的速度大小;
(2)滑块到达A点时对轨道的压力大小;
(3)B、C两点间的高度h.
学校举行遥控赛车比赛。比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L=10m后,由B点进入半径为R=0.4m的光滑竖直圆轨道,离开竖直圆轨道后继续沿光滑平直轨道运动。已知赛车质量m=0.1kg,通电后电机以额定功率P=2.0w工作了t=1.6s后关闭,此时赛车尚未到达B点。赛车到达竖直圆轨道的最高点E时对轨道的压力大小等于赛车的重力。赛车在AB段运动中所受阻力恒定。(取g=10m/s2)求: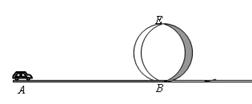
(1)赛车到达竖直圆轨道的最高点E时的速度大小;
(2)赛车在AB段运动时所受阻力的大小.
如图所示,厚度不计的薄板A长L=5.0m,质量M=5.0kg,放在水平桌面上。在A上距右端s=3.0m处放一物体B(大小不计),其质量m=2.0kg,已知A、B间的动摩擦因数μ=0.1,A与桌面间的动摩擦因数μ=0.2,原来系统静止。现在在板的右端施加一大小一定的水平力F=26N,持续作用在A上,将A从B下抽出。(g=10m/s2)求:
(1)A从B下抽出前A、B的加速度各是多少;
(2)B运动多长时间离开A.
如图所示,地面和半圆轨道面PTQ均光滑.质量M=lkg的小车放在地面上,小车上表面与半圆轨道最低点P的切线相平.现有一质量m=2kg的滑块(不计大小)以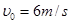 的初速度滑上小车左端,带动小车向右运动,小车跟墙壁碰撞时,滑块处在小车正中间位置且恰好与小车达到共同速度,碰后小车即被粘在墙壁上,滑块最终通过了半圆形轨道的最高点,已知滑块与小车表面的动摩擦因数片
的初速度滑上小车左端,带动小车向右运动,小车跟墙壁碰撞时,滑块处在小车正中间位置且恰好与小车达到共同速度,碰后小车即被粘在墙壁上,滑块最终通过了半圆形轨道的最高点,已知滑块与小车表面的动摩擦因数片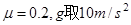

求:(1)小车的长度L;
(2)圆轨道半径R的取值范围.