如图,四棱柱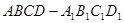 的底面
的底面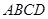 是平行四边形,且
是平行四边形,且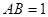 ,
,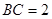 ,
, ,
, 为
为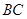 的中点,
的中点, 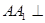 平面
平面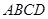 .
.
(1)证明:平面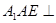 平面
平面 ;
;
(2)若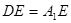 ,试求异面直线
,试求异面直线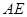 与
与 所成角的余弦值;
所成角的余弦值;
(3)在(2)的条件下,试求二面角 的余弦值.
的余弦值.
(本小题满分12分)
抛物线的顶点在原点,它的准线过双曲线 的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为 ,求抛物线的方程和双曲线的方程。
,求抛物线的方程和双曲线的方程。
(本小题满分12分)
为了美化环境,构建两型社会,市城建局打算在广场上建造一个绚丽多彩的矩形花园,中间有三个完全一样的矩形花坛,每个花坛面积均为294平方米,花坛四周的过道均为
2米,如图所示,设矩形花坛的长为 ,宽为
,宽为 ,整个矩形花园面积为
,整个矩形花园面积为

(1)试用 表示S;
表示S;
(2)为了节约用地,当矩形花坛的长为多少米时,新建矩形花园占地最少,占地多少平米?
(本小题满分12分 )
)
已知直线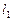 为曲线
为曲线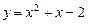 在点
在点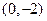 处的切线,
处的切线,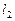 为该曲线的另一条切线,
为该曲线的另一条切线,
且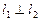 .
.
(Ⅰ )求直线
)求直线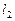 的方程;
的方程;
(Ⅱ)求由直线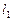 ,
,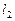 和
和 轴所围成的三角形的面积
轴所围成的三角形的面积
(本小题满分10分)
已知复数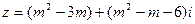 ,则当实数m为何值时,复数z是:
,则当实数m为何值时,复数z是:
①实数; ② ; ③对应的点在第三象限。
; ③对应的点在第三象限。
(本小题满分12分)
已知数列 中,
中,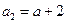 (
( 为常数),
为常数),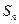 为
为 的前
的前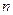 项和,且
项和,且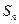 是
是 与
与 的等差中项.
的等差中项.
(Ⅰ)求 ;
;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若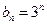 且
且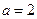 ,
, 为数列
为数列 的前
的前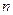 项和,求
项和,求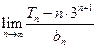 的值.
的值.