已知命题p:函数y=ax+1+1(a>0且a≠1)的图象恒过(﹣1,2)点;命题q:已知平面α∥平面β,则直线m∥α是直线m∥β的充要条件;则下列命题为真命题的是( )
| A.p∧q | B.¬p∧¬q | C.¬p∧q | D.p∧¬q |
设 ,对于数列
,对于数列 ,令
,令 为
为 中的最大值,称数列
中的最大值,称数列 为
为 的“递进上限数列”。例如数列
的“递进上限数列”。例如数列 的递进上限数列为2,2,3,7,7.则下面命题中()
的递进上限数列为2,2,3,7,7.则下面命题中()
①若数列 满足
满足 ,则数列
,则数列 的递进上限数列必是常数列
的递进上限数列必是常数列
②等差数列 的递进上限数列一定仍是等差数列
的递进上限数列一定仍是等差数列
③等比数列 的递进上限数列一定仍是等比数列
的递进上限数列一定仍是等比数列
正确命题的个数是()
| A.0 | B.1 | C.2 | D.3 |
已知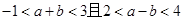 ,则2a+3b的取值范围是()
,则2a+3b的取值范围是()
A.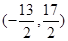 |
B.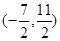 |
C. |
D.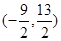 |
等比数列前n项和为Sn,有人算得S1="8," S2="20," S3="36," S4=65,后来发现有一个数算错了,错误的是()
| A.S1 | B.S2 | C.S3 | D.S4 |
已知0<α<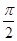 <β<π,又sin α=
<β<π,又sin α= ,cos(α+β)=-
,cos(α+β)=-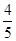 ,则sin β=()
,则sin β=()
A. |
B.0或 |
C.0 | D.0或- |
在 中,若边长和内角满足
中,若边长和内角满足 ,则角
,则角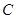 的值是()
的值是()
A. |
B. 或 或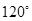 |
C.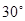 |
D.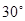 或 或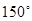 |