（本题10分）△ABC中，∠ACB=90°，AC=BC，AB=2．现将一块三角板的直角顶点放在AB的中点D处，两直角边分别与直线AC、直线BC相交于点E、F．我们把DE⊥AC时的位置定为起始位置（如图1），将三角板绕点D顺时针方向旋转一个角度α （0°＜α＜90°）．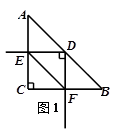
（1）在旋转过程中，当点E在线段AC上，点F在线段BC上时（如图2），
①试判别△DEF的形状，并说明理由；
②判断四边形ECFD的面积是否发生变化，并说明理由．
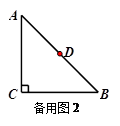
（2）设直线ED交直线BC于点G，在旋转过程中，是否存在点G，使得△EFG为等腰三角形？若存在，求出CG的长，若不存在，说明理由；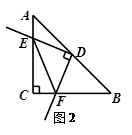
（1）已知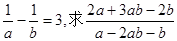
的值
（2） 已知
，求
的值
（1）
（2）
（3）
小斌和小强骑自行车从学校出发去博物馆参观，如果每小时骑10千米，上午10时才能到达，如果每小时15千米，则上午9时30分便可到达，你能算出学校到博物馆的路程吗？
某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
| 与标准质量的差值（单位克） |
-5 |
-2 |
0 |
1 |
3 |
6 |
| 袋数 |
1 |
4 |
3 |
4 |
5 |
3 |
根据上述信息解决如下问题：这批样品的平均质量比标准质量多或少几克？若标准质量为100克，则抽样检测的总质量是多少？
先化简，再求值：4（3x2y-
xy2）-5(xy2+3x2y)，其中x=-1,y=2