阅读理解：
如图1，在四边形ABCD的边AB上任取一点E（点E不与点A．点B重合），分别连接ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．解决问题：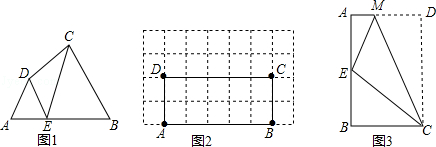
（1）如图1，∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；
（2）如图2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD的边AB上的一个强相似点E；
拓展探究：
（3）如图3，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB和BC的数量关系．
已知，
□ABCD的两边AB、AD的长是关于X的方程x2－mx+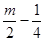
=0的两个实根．
（1）当为何值时，四边形ABCD是菱形？求出这时菱形的边长．
（2）若AB的长为2，那么□ABCD的周长是多少？
如图，自来水公司的主管道从A小区向北偏东60°方向直线延伸，测绘员在A处测得要安装自来水的M小区在A小区北偏东30°方向，测绘员沿主管道步行8000米到达C处，测得小区M位于C的北偏西60°方向，请你（不写作法，保留作图痕迹）找出支管道连接点N，使到该小区铺设的管道最短，并求出AN的长．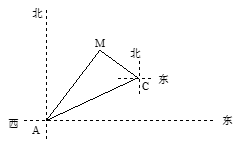
市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
（1）根据表格中的数据，分别计算出甲、乙两人的平均成绩；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
丹东市政府决定，从2011年起在全市开展创建全国文明城市，国家卫生城市，国家环保模范城市，国家园林城市“四城联创”活动.小东同学在全校随机调查了若干名学生对“四城联创”的了解程度，下图是他采集数据后绘制的两幅不完整的统计图（A：不了解，B：一般了解，C：了解较多，D：熟悉）.请你根据图中提供的信息解答以下问题：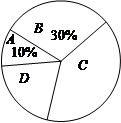
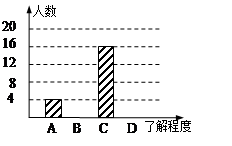
（1）在这次调查活动中，一共调查了多少名学生；
（2）在条形统计图中，将表示B、D的部分补充完整；
（3）在扇形统计图中，计算出C部分所对应的圆心角的度数；
（4）若该校有学生1200名，估计对“四城联创”了解程度为“熟悉” 的学生约有多少名？
如图，已知OB的方向是南偏东60°，OA、OC分别平分∠NOB和∠NOE，
（1）请直接写出OA的方向是__________，OC的方向是__________.
（2）求∠AOC的度数.