在□ABOC中，AO⊥BO，且AO＝BO．以AO、BO所在直线为坐标轴建立如图所示的平面直角坐标系，已知B（－6，0），直线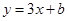过点C且与x轴交于点D．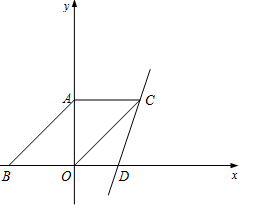

（1）求点D的坐标；
（2）点E为y轴正半轴上一点，当∠BED＝45°时，求直线EC的解析式；
（3）在（2）的条件下，设直线EC与x轴交于点F，ED与AC交于点G．点P从点O出发沿折线OF－FE运动，在OF上的速度是每秒2个单位，在FE上的速度是每秒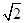个单位．在运动过程中直线PA交BE于H，设运动时间为t．当以E、H、A为顶点的三角形与△EGC相似时，求t的值．

科目 数学   题型 解答题   难度 中等

知识点： 相似多边形的性质 一次函数的最值