杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体（看成一个点）的路线是抛物线，已知起跳点A距地面的高度为1米，弹跳的最大高度距地面4.75米，距起跳点A的水平距离为2.5米，建立如图所示的平面直角坐标系，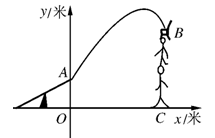
（1）求演员身体运行路线的抛物线的解析式？
（2）已知人梯高BC＝3.4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？说明理由．
解方程：
.
如图，已知抛物线
与x轴的交点为A、D（A在D的右侧），与y轴的交点为C.
（1）直接写出A、D、C三点的坐标；
（2）在抛物线的对称轴上找一点M，使得MD+MC的值最小，并求出点M的坐标；
（3）设点C关于抛物线对称的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，求出点P的坐标；若不存在，请说明理由.
如图，在Rt△ABC中，∠B=90°，AC=60，AB=30。点D是AC上的动点，过D作DF⊥BC于F，再过F作FE//AC，交AB于E。设CD=x，DF=y.
（1）求y与x的函数关系式；
（2）当四边形AEFD为菱形时，求x的值；
（3）当△FED是直角三角形时，求x的值.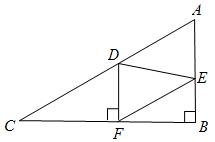
如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE.
（1）求证：CE=CF；
（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
某校为美化校园，计划对面积为1800m2的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m2区域的绿化时，甲队比乙队少用4天.
（1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？
（2）若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？