设a>1,定义 ,如果对任意的n∈N*且n≥2,不等式12f(n)+7logab>7loga+1b+7(a>0且a≠1)恒成立,则实数b的取值范围是( )
,如果对任意的n∈N*且n≥2,不等式12f(n)+7logab>7loga+1b+7(a>0且a≠1)恒成立,则实数b的取值范围是( )
A. |
B.(0,1) | C.(0,4) | D.(1,+∞) |
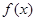 是定义在(0,
是定义在(0,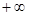 )上的非负可导函数,且满足
)上的非负可导函数,且满足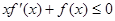 .对任意正数
.对任意正数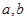 ,若
,若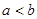 ,则必有()
,则必有()
A.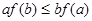 |
B.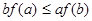 |
C.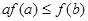 |
D.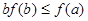 |
以下四图,都是同一坐标系中三次函数及其导函数的图像,其中一定不正确的序号是 ()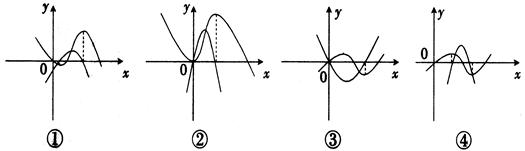
| A.①、② | B.①、③ | C.③、④ | D.①、④ |
设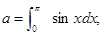 则二项式
则二项式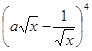 的展开式的常数项是()
的展开式的常数项是()
| A.24 | B.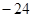 |
C.48 | D.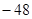 |
若实数a,b,c满足|a-c|<|b|,则下列不等式中成立的是( )
| A.|a|>|b|-|c| | B.|a|<|b|+|c| | C.a>c-b | D.a<b+c |
为了创建全国卫生城市,在湛江市民中选8名青年志愿者,其中有3名男青年志愿者,5名女青年志愿者,现从中选3人参加“创建全国卫生城市”户外活动导引工作,则这3人中既有男青年志愿者又有女青年志愿者的概率为( )
A. |
B.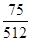 |
C. |
D. |