（本小题满分12分）某校学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：
（1）指出这组数据的众数和中位数；
（2）若幸福度不低于9．5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记X表示抽到“极幸福”的人数，求X的分布列及数学期望．
.
设数列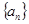
满足
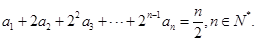
（1）求数列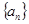的通项公式；
（2）设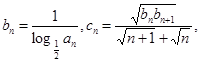
记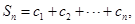
证明：Sn＜1.
（本小题满分14分）
已知抛物线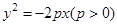
的焦点为
F，过F的直线交y轴正半轴于点，交抛物线于A，B两点，其中A在第二象限。
（1）求证：以线段FA为直径为圆与Y轴相切；
（2）若
，求
的值.
（本小题满分12分）
已知函数
，（K常数）
（1）求函数f(x)的单调区间；
（2）若
恒成立，求K的取值范围。
（本小题满分12分)
已知数列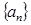
的前n项和为
，
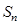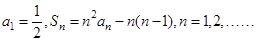
（1）证明：数列
是等差数列，并求；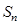
（2）设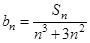
，求证：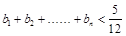
.
（本小题满分12分）
设椭圆E：
的上焦点是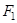
，过点P（3，4）和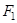作直线P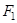交椭圆于A、B两点，已知A(
).
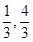(1)求椭圆E的方程；
(2)设点C是椭圆E上到直线P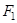距离最远的点，求C点的坐标。