（本小题满分13分）某同学用“五点法”画函数
在某一个周期内的图象时，列表并填入的部分数据如下表:
（Ⅰ）请求出上表中的
，并直接写出函数
的解析式；
（Ⅱ）将的图象沿
轴向右平移
个单位得到函数
，若函数在
（其中
）上的值域为
，且此时其图象的最高点和最低点分别为
，求
与
夹角
的大小。
某公司试销一种新产品，规定试销时销售单价不低于成本单价500元/件，又不高于800元/件，经试销调查，发现销售量y（件）与销售单价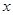
（元/件）之间，可近似看做一次函数
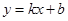的关系（图象如图所示）．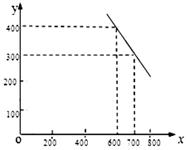
（1）根据图象，求一次函数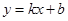的表达式；
（2）设公司获得的毛利润（毛利润＝销售总价－成本总价）为S元：
①求S关于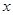的函数表达式；
②求该公司可获得的最大毛利润，并求出此时相应的销售单价．
已知函数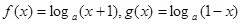
，
其中（
且
⑴求函数
的定义域；
⑵判断函数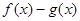
的奇偶性，并予以证明；
⑶判断它在区间（0,1）上的单调性并说明理由。
（1）求函数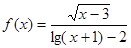
的定义域；
（2）求函数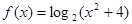
的值域；
（1）已知二次函数
，求
的单调递减区间。
（2）
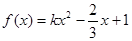在区间
上单调递减，求实数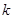
的取值范围。
已知函数f(x)=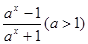
,
(1)判断函数的奇偶性；(2)证明f(x)是R上的增函数； (3)求该函数的值域；