（本小题满分14分）已知函数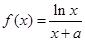
(
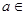R)，曲线
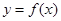在点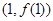
处的切线方程为
.
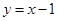(1)求实数a的值，并求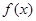
的单调区间；
(2)试比较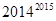
与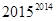
的大小，并说明理由；
(3)是否存在k∈Z，使得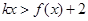
对任意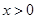
恒成立？若存在，求出k的最小值；若不存在，请说明理由.
（本小题满分14分）若卫星运行轨道椭圆
的离心率为
，地
心为右焦点
，
（1）求椭圆方程 ；
（2）若P为椭圆上一动点，求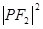
的最小值。
（本小题满分12分）在
中，
是三角形的三内角，
是三内角对应的三边，已知
．
（1）求角
的大小；
（2）若
，求角
的大小．
（本小题满分12分）已知圆C：
，
求：(1) 圆C的半径；
(2) 若直线
与圆C有两个不同的交点，求
的取值范围．
已知椭圆C的两焦点分别为
，长轴长为6，
(1)求椭圆C的标准方程;
(2)已知过点(0,0)且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度
（满分14 分）已知抛物线
，焦点为F，顶点为原点O，
（1）求抛物线的焦点坐标准线方程；
（2）若P(a,4)，求Q到F的距离；
（3）若点P在抛物线上移动，M是OP的中点，求点M的轨迹方程．