(本小题满分14分)已知函数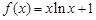 ,
,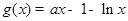
(Ⅰ)求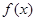 的最小值;
的最小值;
(Ⅱ)讨论函数 的单调性;
的单调性;
(Ⅲ)是否存在常数 ,使
,使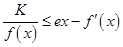 恒成立,若存在,求出
恒成立,若存在,求出 的最大值,若不存在,说明理由.
的最大值,若不存在,说明理由.
已知离心率为 的椭圆
的椭圆 的顶点
的顶点 恰好是双曲线
恰好是双曲线 的左右焦点,点
的左右焦点,点 是椭圆
是椭圆 上不同于
上不同于 的任意一点,设直线
的任意一点,设直线 的斜率分别为
的斜率分别为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)当 ,在焦点在
,在焦点在 轴上的椭圆
轴上的椭圆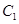 上求一点Q,使该点到直线(
上求一点Q,使该点到直线(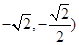 的距离最大。
的距离最大。
(3)试判断乘积“(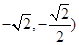 ”的值是否与点(
”的值是否与点(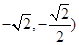 的位置有关,并证明你的结论;
的位置有关,并证明你的结论;
双曲线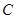 的中心在原点,右焦点为
的中心在原点,右焦点为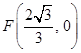 ,渐近线方程为
,渐近线方程为 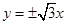 .
.
(1)求双曲线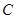 的方程;
的方程;
(2)设直线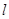 :
: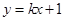 与双曲线
与双曲线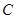 交于
交于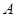 、
、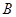 两点,问:当
两点,问:当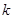 为何值时,以
为何值时,以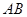 为直径的圆过原点;
为直径的圆过原点;
已知p: 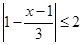 ,q:
,q: 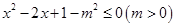 ,若
,若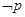 是
是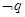 的必要不充分条件,求实数m的取值范围。
的必要不充分条件,求实数m的取值范围。
已知点A(1,0)及圆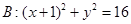 ,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。
,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。
已知函数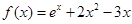 .
.
(1)求证:函数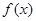 在区间
在区间 上存在唯一的极值点;
上存在唯一的极值点;
(2)当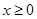 时,若关于
时,若关于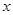 的不等式
的不等式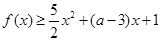 恒成立,试求实数
恒成立,试求实数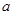 的取值范围.
的取值范围.