已知离心率为
的椭圆的顶点恰好是双曲线的左右焦点，点是椭圆上不同于的任意一点，设直线的斜率分别为.
（1）求椭圆的标准方程；
（2）当，在焦点在轴上的椭圆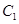
上求一点Q，使该点到直线（
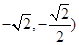的距离最大。
（3）试判断乘积“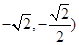（”的值是否与点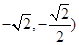（的位置有关，并证明你的结论；
设
，求函数
的最小值及相应
的值．
已知椭圆
的离心率为
，定点M（1，0），椭圆短轴的端点是B1，B2，且
（1）求椭圆C的方程；
（2）设过点M且斜率不为0的直线交椭圆C于A，B两点．试问x轴上是否存在定点P，使PM平分∠APB?若存在，求出点P的坐标；若不存在，说明理由，
已知函数
．
（1）若函数f（x）的图象在
处的切线斜率为3，求实数m的值；
（2）求函数f（x）的单调区间；
（3）若函数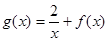
在[1，2]上是减函数，求实数m的取值范围．
数列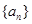
为正项等比数列，且满足
；设正项数列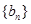
的前n项和为Sn，满足
．
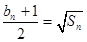（1）求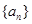的通项公式；
（2）设
的前项的和Tn．
如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA1平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．
（1）证明：AE⊥PD‘
（2）若H为PD上的动点，EH与平面PAD所成最大角的正切值为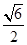
求二面角E-AF-C的余弦值