数列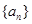 为正项等比数列,且满足
为正项等比数列,且满足 ;设正项数列
;设正项数列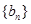 的前n项和为Sn,满足
的前n项和为Sn,满足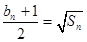 .
.
(1)求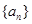 的通项公式;
的通项公式;
(2)设 的前项的和Tn.
的前项的和Tn.
某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构。若甲、乙、丙、丁4名参加保险人员所在地区附近有A、B、C三家社区医院,并且他们的选择是相互独立的。
(Ⅰ)求甲、乙两人都选择A社区医院的概率;
(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;
(Ⅲ)设4名参加保险人员中选择A社区医院的人数为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
在直角坐标平面内,以坐标原点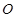 为极点,
为极点,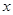 轴的非负半轴为极轴建立极坐标系。已知点
轴的非负半轴为极轴建立极坐标系。已知点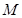 的极坐标为
的极坐标为 ,曲线
,曲线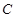 的参数方程为
的参数方程为 (
(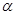 为参数)。
为参数)。
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求点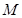 到曲线
到曲线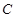 上的点的距离的最小值。
上的点的距离的最小值。
用适当方法证明:如果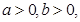 那么
那么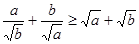 。
。
已知函数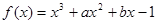 在
在 处有极值
处有极值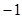 。
。
(Ⅰ)求实数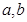 的值;
的值;
(Ⅱ)求函数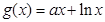 的单调区间。
的单调区间。
一个口袋中装有大小相同的2个白球和3个黑球。
(Ⅰ)从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率。