(本小题满分10分)
已知f(x)=2x+a,g(x)=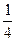 (3+x2),若g[f(x)]=x2+x+1,求a的值。
(3+x2),若g[f(x)]=x2+x+1,求a的值。
如图A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A、B的任一点,AA1=AB=2
⑴求证:BC⊥平面A1AC
⑵求三棱锥A1—ABC体积的最大值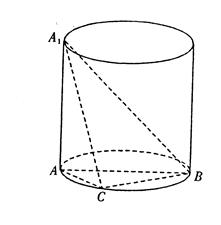
已知半径为2cm的半圆形铁皮,用它做成一个圆锥形容器的侧面
⑴求这个圆锥的体积
⑵经过它的侧面,用细绳把A、B连接起来,
则细绳至少要多长?(AB为圆锥底面圆的直径)
已知 ,
,
⑴若 ,求
,求
⑵若 (其中O为坐标原点),求
(其中O为坐标原点),求
已知等差数列 的各项均为正数,
的各项均为正数, ,前
,前 项和为
项和为 为等比数列,公比
为等比数列,公比 ;(1)求
;(1)求 与
与 ;(2)求数列
;(2)求数列 的前
的前 项和
项和 ;(3)记
;(3)记 对任意正整数
对任意正整数 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
在△ABC中,a, b, c分别为内角A, B, C的对边,且
(1).求A的大小(2).求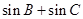 的最大值.
的最大值.